2021-09-12

SpringBoot

Spring Boot 是一个用于简化 Spring 应用程序开发的框架，它提供了大量的注解来简化配置和开发。

SpringFramework没有解决了什么问题？

为什么有了SpringFramework还会诞生SpringBoot？简单而言，因为虽然Spring的组件代码是轻量级的，但它的配置却是重量级的。
一开始，Spring用XML配置，而且是很多XML配置。Spring 2.5引入了基于注解的组件扫描，这消除了大量针对应用程序自身组件的显式XML配置。Spring 3.0引入了基于Java的配置，这是一种类型安全的可重构配置方式，可以代替XML。
所有这些配置都代表了开发时的损耗。因为在思考Spring特性配置和解决业务问题之间需要进行思维切换，所以编写配置挤占了编写应用程序逻辑的时间。和所有框架一样，Spring实用，但与此同时它要求的回报也不少。
除此之外，项目的依赖管理也是一件耗时耗力的事情。在环境搭建时，需要分析要导入哪些库的坐标，而且还需要分析导入与之有依赖关系的其他库的坐标，一旦选错了依赖的版本，随之而来的不兼容问题就会严重阻碍项目的开发进度。
1.jsp中要写很多代码、控制器过于灵活,缺少一个公用控制器 2.Spring不支持分布式,这也是EJB仍然在用的原因之一。

SringBoot的概述

SpringBoot解决上述Spring的缺点
SpringBoot对上述Spring的缺点进行的改善和优化，基于约定优于配置的思想，可以让开发人员不必在配置与逻辑业务之间进行思维的切换，全身心的投入到逻辑业务的代码编写中，从而大大提高了开发的效率，一定程度上缩短了项目周期。
SpringBoot的特点
1、为基于Spring的开发提供更快的入门体验
2、开箱即用，没有代码生成，也无需XML配置。同时也可以修改默认值来满足特定的需求
3、提供了一些大型项目中常见的非功能性特性，如嵌入式服务器、安全、指标，健康检测、外部配置等
SpringBoot不是对Spring功能上的增强，而是提供了一种快速使用Spring的方式
SpringBoot的核心功能
- 起步依赖：起步依赖本质上是一个Maven项目对象模型（Project Object Model，POM），定义了对其他库的传递依赖，这些东西加在一起即支持某项功能。简单的说，起步依赖就是将具备某种功能的坐标打包到一起，并提供一些默认的功能。
- 自动配置：Spring Boot的自动配置是一个运行时（更准确地说，是应用程序启动时）的过程，考虑了众多因素，才决定Spring配置应该用哪个，不该用哪个。该过程是Spring自动完成的
为什么添加一个starter-web模块，一个简单的web程序便完成了呢？
SpringBoot最强大的地方在于约定大于配置，只要你引入某个模块的xx-start包，它将自动注入配置，提供了这个模块的功能；
比如这里我们在POM中添加了如下的包
1
2
3
4
<dependency>
<groupId>org.springframework.boot</groupId>
<artifactId>spring-boot-starter-web</artifactId>
</dependency>
它内嵌了Tomcat并且提供了默认的配置，比如默认端口是8080；可以在application.properties或者application.yml中修改配置。

SpringBoot 注解

@SpringBootApplication：该注解用于标记主应用程序类，通常位于项目的顶层包中。定义在main方法入口类处，用于启动sping boot应用项目。
它包含了 @Configuration、@EnableAutoConfiguration 和 @ComponentScan 注解，用于自动配置和组件扫描。

@Target(ElementType.TYPE)
@Retention(RetentionPolicy.RUNTIME)
@Documented
@Inherited
@Configuration
@EnableAutoConfiguration
@ComponentScan
public @interface SpringBootApplication {

	/**
	 * Exclude specific auto-configuration classes such that they will never be applied.
	 * @return the classes to exclude
	 */
	Class<?>[] exclude() default {};

}

@EnableAutoConfiguration：让spring boot根据类路径中的jar包依赖当前项目进行自动配置，在src/main/resources的META-INF/spring.factories

@ImportResource：加载xml配置，一般是放在启动main类上
@ConfigurationProperties(prefix="person")：可以新建一个properties文件，ConfigurationProperties的属性prefix指定properties的配置的前缀，通过location指定properties文件的位置
@PostConstruct：spring容器初始化时，要执行该方法
@ComponentScan：注解会告知Spring扫描指定的包来初始化Spring

@RestController：用于标记一个类，表示它是一个控制器类，处理 HTTP 请求并返回 JSON 或 XML 等数据。
@GetMapping、@PostMapping、@PutMapping、@DeleteMapping：这些注解分别用于将 HTTP GET、POST、PUT 和 DELETE 请求映射到相应的处理方法上。
@RequestMapping：用于将 HTTP 请求映射到控制器方法上，指定请求的 URL 路径和请求方法（GET、POST、PUT、DELETE 等）

1	@RequestMapping(path = "/user/detail", method = RequestMethod.POST)

@RequestParam：用于从请求参数中获取值，并将其传递给控制器方法的参数。

public List<CopperVO> getOpList(HttpServletRequest request,
                                @RequestParam(value = "pageIndex", required = false) Integer pageIndex,
                                @RequestParam(value = "pageSize", required = false) Integer pageSize) {

}

@PathVariable：用于从 URL 路径中获取值，并将其传递给控制器方法的参数。
@RequestBody：用于将请求体中的数据绑定到控制器方法的参数上，通常用于接收 JSON 或 XML 数据。
@ResponseBody：表示方法返回的对象应该直接写入HTTP响应体，而不是通过视图解析器进行渲染。
@Autowired 是 Spring 框架自带的注解用于进行依赖注入，将 Spring 托管的 bean 注入到需要它们的类中。
@Resource是 Java EE 提供的注解，用于实现依赖注入。它可以用于字段、setter 方法、构造函数等地方，用于告诉容器注入指定名称或类型的 bean。
@Bean：用于定义Spring Bean，通常在 @Configuration 类中使用。
@Component 是 Spring 框架中用于声明一个类为 Spring 管理的组件（Bean）的注解。
@Service、@Repository、@Controller：这些注解分别用于标记服务类、仓库类和控制器类，以便 Spring Boot 可以自动扫描并创建这些组件。都属于 @Component 的衍生注解，用于更明确地表示类的职责。
@Configuration：用于定义配置类，通常与 @Bean 注解一起使用，用于配置第三方库或复杂的 bean。
@Override 是Java中的一个注解（Annotation），用于标识方法是否是一个覆盖（重写）了父类或接口中的方法。它提供了编译时的检查，确保您正确地重写了父类或接口中的方法，以防止由于拼写错误或方法签名不匹配而导致的错误。
@Value：用于注入属性值，从配置文件中获取属性值。
@Profile：用于定义不同环境下的配置文件，可以根据不同的配置文件加载不同的配置。
@Conditional：用于根据条件决定是否创建某个 bean。
@Param：给参数变量起别名。如果只有一个参数，并且在mapper对应的xml文件中里使用，则必须加别名。
@Async 是 Spring 框架中用于实现异步方法调用的注解。通过在方法上添加 @Async 注解，Spring Boot 就会在调用该方法时使用另一个线程来执行，而不是阻塞当前线程等待方法执行完成。
@Order：如 @Order(1)，值越小优先级超高，越先运行

2021-09-11

Spring 🍃

Spring 是一个开源的轻量级框架，用于构建企业级 Java 应用程序。它提供了广泛的基础设施支持和许多可重用的库，以简化企业级应用程序的开发。Spring 框架的设计目标是促进松耦合、可维护性和可测试性的编码实践。
Spring的一个最大的目的就是使 JAVA EE 开发更加容易。同时，Spring之所以与Struts、Hibernate等单层框架不同，是因为Spring致力于提供一个以统一的、高效的方式构造整个应用，并且可以将单层框架以最佳的组合揉和在一起建立一个连贯的体系。可以说Spring是一个提供了更完善开发环境的一个框架，可以为POJO对象提供企业级的服务。

官方的项目和教程地址，在学习Spring时，一定要把它当做生态体系，而是不是一个简单的开发框架。
Spring简单例子引入Spring要点：https://pdai.tech/md/spring/spring-x-framework-helloworld.html

核心功能和特点

非侵入式：基于Spring开发的应用中的对象可以不依赖于Spring的API
控制反转（IoC）：Inversion of Control，指的是将对象的创建权交给 Spring 去创建。Spring 的 IoC 容器管理对象的生命周期和配置，开发者不再需要手动 new创建对象。这种反转控制的方式使得应用程序更加松散耦合、易于测试和维护。Spring 管理一切，管理项目中的对象和整合其他对象。
依赖注入：DI——Dependency Injection，是指依赖的对象不需要手动调用 setXX 方法去设置，而是通过配置赋值。
面向切面编程（AOP）：Spring 提供了强大的 AOP 支持，通过 AOP 可以更好地处理横切关注点，如事务管理、安全性、日志记录等。AOP 可以提高代码的模块性和可维护性。
容器：Spring 是一个容器，因为它包含并且管理应用对象的生命周期
组件化：Spring 实现了使用简单的组件配置组合成一个复杂的应用。在 Spring 中可以使用XML和Java注解组合这些对象。
一站式：在 IOC 和 AOP 的基础上可以整合各种企业应用的开源框架和优秀的第三方类库（实际上 Spring 自身也提供了表现层的 SpringMVC 和持久层的 Spring JDBC）
- 模型视图控制器（MVC）：Spring MVC 是一个强大的 Web 框架，通过注解配置和可插拔的视图解析器简化了 Web 应用的开发。它提供了清晰的分层结构，使得开发更加模块化。
- Spring 简化了数据访问的过程，提供了一致的编程模型，支持 JDBC 和 ORM 框架。这使得数据访问更加灵活、简单，且易于集成各种数据源。
- Spring 真正的利用了一些现有的技术，像 ORM 框架、日志框架、JEE、Quartz 和 JDK 计时器，其他视图技术。
- Spring 对 JavaEE 开发中非常难用的一些 API（JDBC、JavaMail、远程调用等）都提供了封装，使这些API应用难度大大降低。
事务管理：Spring 提供了声明式事务管理，通过注解或 XML 配置来管理事务。这样可以将事务管理从业务代码中解耦，使代码更加干净和易于理解。Spring 提供了一致的事务管理接口，可向下扩展到（使用一个单一的数据库，例如）本地事务并扩展到全局事务（例如，使用 JTA）
灵活性和可扩展性：Spring 的模块化结构使得可以仅使用需要的功能，从而保持应用程序的轻量级。Spring 的组件是可插拔的，可以轻松地集成第三方库。
- ？？Spring 可以使开发人员使用 POJOs（Plain old Java object）开发企业级的应用程序。只使用 POJOs 的好处是你不需要一个 EJB 容器产品，比如一个应用程序服务器，但是你可以选择使用一个健壮的 servlet 容器，比如 Tomcat 或者一些商业产品。
- Spring 在一个单元模式中是有组织的。即使包和类的数量非常大，你只要担心你需要的，而其它的就可以忽略了。
- 轻量级的 IOC 容器往往是轻量级的，例如，特别是当与 EJB 容器相比的时候。这有利于在内存和 CPU 资源有限的计算机上开发和部署应用程序。
测试支持：Spring 框架鼓励并支持测试驱动开发(TDD)。提供许多工具和类库来进行单元测试和集成测试，保障应用程序的质量。
？？测试一个用 Spring 编写的应用程序很容易，因为环境相关的代码被移动到这个框架中。此外，通过使用 JavaBean-style POJOs，它在使用依赖注入注入测试数据时变得更容易。

Spring Framework

下图来自官方文档 Spring-framework 5.0；需要注意的是，虽然这个图来源于Spring Framwork5.0 M4 版本，但是它依然是V4版本的图，比如Spring 5版本中的web模块已经去掉了Portlet模块，新增了WebFlux模块等。
包含了 Spring 框架的所有模块，可以满足一切企业级应用开发的需求，在开发过程中可以根据需求有选择性地使用所需要的模块。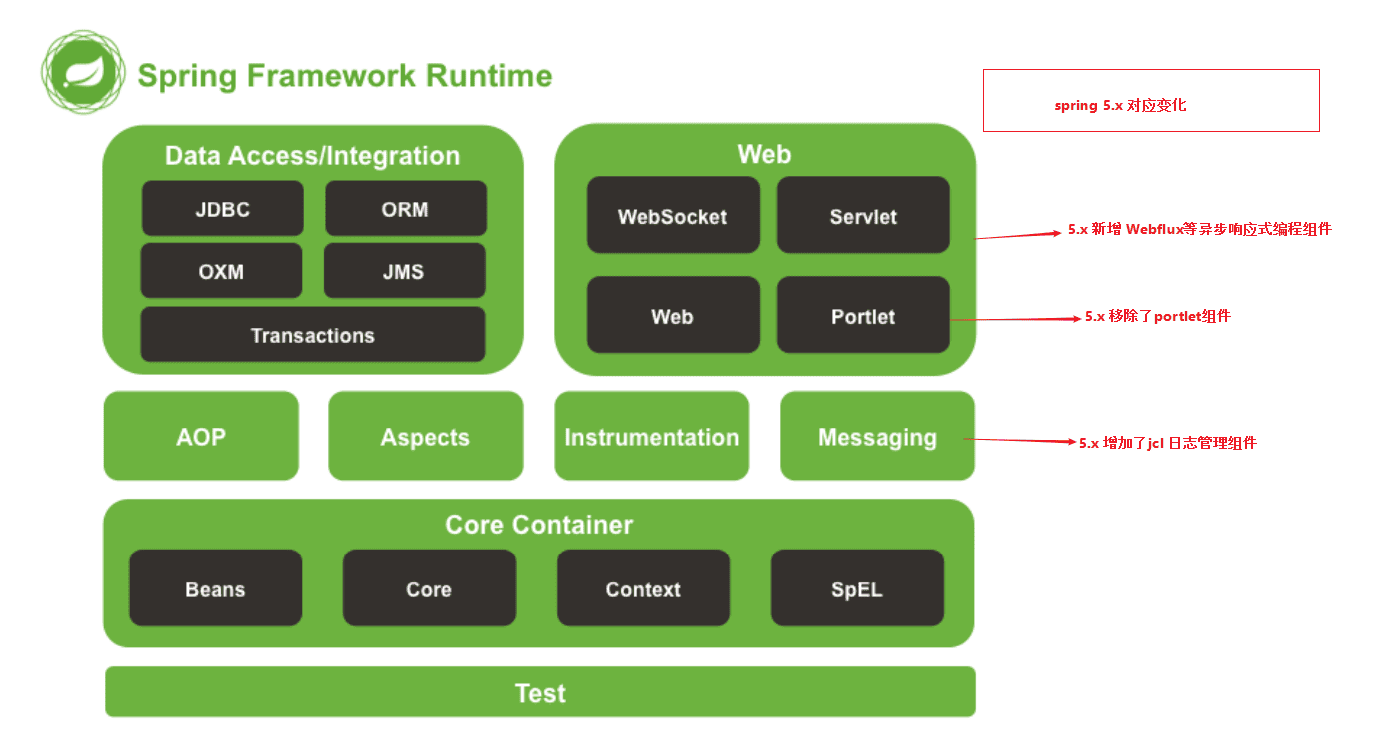

Core Container（Spring的核心容器）

Spring 的核心容器是其他模块建立的基础，没有这些核心容器，也不可能有 AOP、Web 等上层的功能。

Beans 模块：提供了框架的基础部分，包括控制反转和依赖注入。
Core 核心模块：封装了 Spring 框架的底层部分，包括资源访问、类型转换及一些常用工具类。
Context 上下文模块：建立在 Core 和 Beans 模块的基础之上，集成 Beans 模块功能并添加资源绑定、数据验证、国际化、Java EE 支持、容器生命周期、事件传播等。ApplicationContext 接口是上下文模块的焦点。
SpEL 模块：提供了强大的表达式语言支持，支持访问和修改属性值，方法调用，支持访问及修改数组、容器和索引器，命名变量，支持算数和逻辑运算，支持从 Spring 容器获取 Bean，它也支持列表投影、选择和一般的列表聚合等。

Data Access/Integration（数据访问／集成）

JDBC 模块：提供了一个 JDBC 的样例模板，使用这些模板能消除传统冗长的 JDBC 编码还有必须的事务控制，而且能享受到 Spring 管理事务的好处。
ORM 模块：提供与流行的“对象-关系”映射框架无缝集成的 API，包括 JPA、JDO、Hibernate 和 MyBatis 等。而且还可以使用 Spring 事务管理，无需额外控制事务。
OXM 模块：提供了一个支持 Object /XML 映射的抽象层实现，如 JAXB、Castor、XMLBeans、JiBX 和 XStream。将 Java 对象映射成 XML 数据，或者将XML 数据映射成 Java 对象。
JMS 模块：指 Java 消息服务，提供一套 “消息生产者、消息消费者”模板用于更加简单的使用 JMS，JMS 用于用于在两个应用程序之间，或分布式系统中发送消息，进行异步通信。
Transactions 事务模块：支持编程和声明式事务管理。

Web模块

Web 模块：提供了基本的Web开发集成特性，例如多文件上传功能、使用的 Servlet监听器的IOC容器初始化以及Web应用上下文。
Servlet 模块：提供了一个 Spring MVC Web 框架实现。Spring MVC 框架提供了基于注解的请求资源注入、更简单的数据绑定、数据验证等及一套非常易用的 JSP 标签，完全无缝与 Spring 其他技术协作。
WebSocket 模块：提供了简单的接口，用户只要实现响应的接口就可以快速的搭建 WebSocket Server，从而实现双向通讯。
Webflux 模块： Spring WebFlux 是 Spring Framework 5.x中引入的新的响应式web框架。与Spring MVC不同，它不需要Servlet API，是完全异步且非阻塞的，并且通过Reactor项目实现了Reactive Streams规范。Spring WebFlux 用于创建基于事件循环执行模型的完全异步且非阻塞的应用程序。

AOP、Aspects、Instrumentation 和 Messaging

AOP 模块：提供了面向切面编程实现，提供比如日志记录、权限控制、性能统计等通用功能和业务逻辑分离的技术，并且能动态的把这些功能添加到需要的代码中，这样各司其职，降低业务逻辑和通用功能的耦合。

AOP：即面向方面（切面）编程。是一种编程思想，是对OOP的补充，可以进一步提高编程的效率。
例如，把多个业务组件的共同功能封装成一个“系统组件”，如对所有service类进行权限检查、记录日志、事务管理…
织入：将方面Aspect（处理系统组件的额外的bean）[切点Pointcut（声明织入到哪些对象的哪些位置）+ 通知Advice（处理的逻辑(前,后,返回,异常)] —> 织入Weaving（编译时/装载时/运行时） —> 目标对象Target（程序中开发好的bean）的连接点Joinpoint（可以织入代码的地方）
AOP的实现
- AspectJ：语言级的实现（一门新语言）。编译期织入代码。
- Spring AOP：纯Java实现。运行时通过代理的方式织入代码，只支持方法类型的连接点。
  - JDK动态代理：在运行时创建接口的代理实例。Spring AOP 默认方式，在接口的代理实例中织入代码。
  - CGLib动态代理：不要求目标类实现接口，通过继承目标类来创建代理对象。即可以代理没有实现接口的类。
  - 如果你的目标类已经实现了接口，并且你希望代理对象是目标类的接口的实现，那么可以使用JDK动态代理。如果你的目标类没有实现接口，或者你需要代理非公共方法（final、private等），那么可以使用CGLib动态代理。

@Component
@Aspect
public class ServiceLogAspect {
    // 切点：service包下的所有方法
    @Pointcut("execution(* com.nowcoder.community.service.*.*(..))")
    public void pointcut() {}
    // 前置通知
    @Before("pointcut()")
    public void before(JoinPoint joinPoint) {
        // 用户[1.2.3.4],在[xxx],访问了[com.nowcoder.community.service.xxx()].
        ServletRequestAttributes attributes = (ServletRequestAttributes) RequestContextHolder.getRequestAttributes();
        HttpServletRequest request = attributes.getRequest();
        String ip = request.getRemoteHost();
        String now = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss").format(new Date());
        String target = joinPoint.getSignature().getDeclaringTypeName() + "." + joinPoint.getSignature().getName();
        logger.info(String.format("用户[%s],在[%s],访问了[%s].", ip, now, target));    
    }  }

Aspects 模块：提供与 AspectJ 的集成，是一个功能强大且成熟的面向切面编程（AOP）框架。
Instrumentation 模块：提供了类工具的支持和类加载器的实现，可以在特定的应用服务器中使用。
messaging 模块：Spring 4.0 以后新增了消息（Spring-messaging）模块，该模块提供了对消息传递体系结构和协议的支持。
jcl 模块： Spring 5.x中新增了日志框架集成的模块。

Test模块

Spring 支持 Junit 和 TestNG 测试框架，而且还额外提供了一些基于 Spring 的测试功能，比如在测试 Web 框架时，模拟 Http 请求的功能。包含Mock Objects, TestContext Framework, Spring MVC Test, WebTestClient。

结合Spring历史版本和SpringBoot看发展

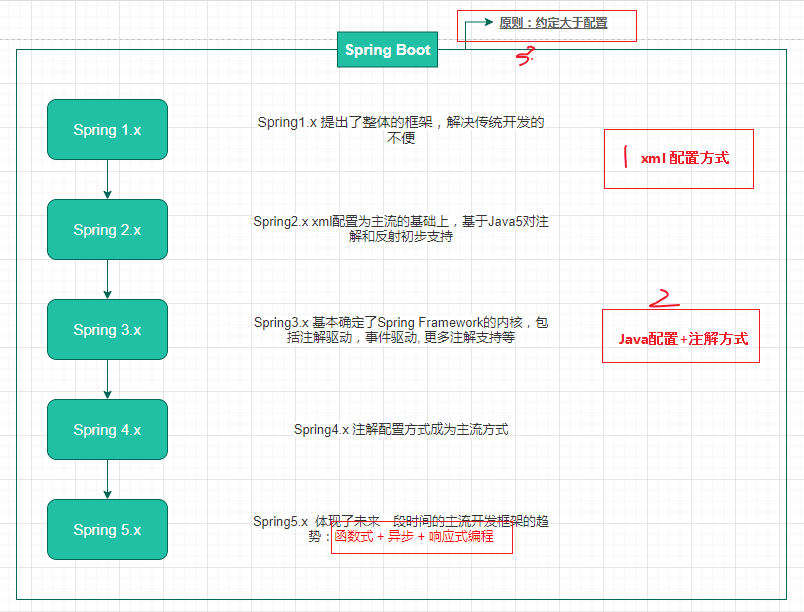
控制反转(IOC)

IoC Container管理的是Spring Bean，那么Spring Bean是什么呢？
Spring里面的bean就类似是定义的一个组件，而这个组件的作用就是实现某个功能的，这里所定义的bean就相当于给了你一个更为简便的方法来调用这个组件去实现你要完成的功能。
Ioc—Inversion of Control，即“控制反转”，不是什么技术，而是一种设计思想。
在Java开发中，Ioc意味着将你设计好的对象交给容器控制，而不是传统的在你的对象内部直接控制。
- 谁控制谁，控制什么？传统Java SE程序设计，我们直接在对象内部通过new进行创建对象，是程序主动去创建依赖对象；而IoC是有专门一个容器来创建这些对象，即由Ioc容器来控制对象的创建；
  - 谁控制谁？当然是IoC 容器控制了对象；
  - 控制什么？那就是主要控制了外部资源获取（不只是对象包括比如文件等）。？？？？？？？？
- 为何是反转，哪些方面反转了?有反转就有正转，传统应用程序是由我们自己在对象中主动控制去直接获取依赖对象，也就是正转；而反转则是由容器来帮忙创建及注入依赖对象；
  - 为何是反转？因为由容器帮我们查找及注入依赖对象，对象只是被动的接受依赖对象，所以是反转；
  - 哪些方面反转了？依赖对象的获取被反转了。

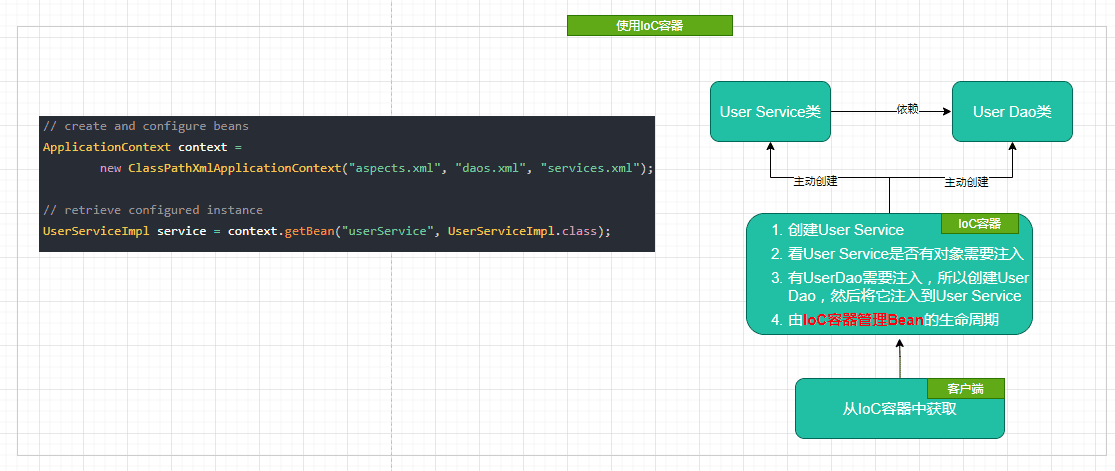
IoC能做什么？
IoC 不是一种技术，只是一种思想，一个重要的面向对象编程的法则，它能指导我们如何设计出松耦合、更优良的程序。
传统应用程序都是由我们在类内部主动创建依赖对象，从而导致类与类之间高耦合，难于测试；有了IoC容器后，把创建和查找依赖对象的控制权交给了容器，由容器进行注入组合对象，所以对象与对象之间是松散耦合，这样也方便测试，利于功能复用，更重要的是使得程序的整个体系结构变得非常灵活。
其实IoC对编程带来的最大改变不是从代码上，而是从思想上，发生了“主从换位”的变化。应用程序原本是老大，要获取什么资源都是主动出击，但是在IoC/DI思想中，应用程序就变成被动的了，被动的等待IoC容器来创建并注入它所需要的资源了。
IoC和DI是什么关系？
控制反转是通过依赖注入实现的，其实它们是同一个概念的不同角度描述。通俗来说就是IoC是设计思想，DI是实现方式。
DI—Dependency Injection：组件之间依赖关系由容器在运行期决定，形象的说，即由容器动态的将某个依赖关系注入到组件之中。依赖注入的目的并非为软件系统带来更多功能，而是为了提升组件重用的频率，并为系统搭建一个灵活、可扩展的平台。通过依赖注入机制，我们只需要通过简单的配置，而无需任何代码就可指定目标需要的资源，完成自身的业务逻辑，而不需要关心具体的资源来自何处，由谁实现。？？？？？
谁依赖于谁？当然是应用程序依赖于IoC容器；？？？？！！！！！！！
为什么需要依赖？应用程序需要IoC容器来提供对象需要的外部资源；
谁注入谁？很明显是IoC容器注入应用程序某个对象，应用程序依赖的对象；
注入了什么？就是注入某个对象所需要的外部资源（包括对象、资源、常量数据）。
Ioc 配置的三种方式
- xml 配置：就是将bean的信息配置.xml文件里，通过Spring加载文件为我们创建bean。这种方式出现很多早前的SSM项目中，将第三方类库或者一些配置工具类都以这种方式进行配置，主要原因是由于第三方类不支持Spring注解。
- Java 配置：将类的创建交给我们配置的JavcConfig类来完成，Spring只负责维护和管理，采用纯Java创建方式。其本质上就是把在XML上的配置声明转移到Java配置类中
- 注解配置：通过在类上加注解的方式，来声明一个类交给Spring管理，Spring会自动扫描带有@Component，@Controller，@Service，@Repository这四个注解的类，然后帮我们创建并管理，前提是需要先配置Spring的注解扫描器。设置ComponentScan的basePackage, 比如 context:component-scan base-package=’tech.pdai.springframework’>, 或者@ComponentScan(“tech.pdai.springframework”)注解，或者 new AnnotationConfigApplicationContext(“tech.pdai.springframework”)指定扫描的basePackage.
依赖注入的三种方式
- 构造方法注入（Construct注入）
- setter注入
- 基于注解的注入（接口注入）
  、、？？

切面编程(AOP)

https://pdai.tech/md/spring/spring-x-framework-aop.html

、、

SpringMVC请求流程和案例

什么是MVC
MVC英文是Model View Controller，是模型(model)－视图(view)－控制器(controller)的缩写，一种软件设计规范。本质上也是一种解耦。用一种业务逻辑、数据、界面显示分离的方法，将业务逻辑聚集到一个部件里面，在改进和个性化定制界面及用户交互的同时，不需要重新编写业务逻辑。MVC被独特的发展起来用于映射传统的输入、处理和输出功能在一个逻辑的图形化用户界面的结构中。
Model（模型）是应用程序中用于处理应用程序数据逻辑的部分。通常模型对象负责在数据库中存取数据。
View（视图）是应用程序中处理数据显示的部分。通常视图是依据模型数据创建的。
Controller（控制器）是应用程序中处理用户交互的部分。通常控制器负责从视图读取数据，控制用户输入，并向模型发送数据。
什么是Spring MVC？
简单而言，Spring MVC是Spring在Spring Container Core和AOP等技术基础上，遵循上述Web MVC的规范推出的web开发框架，目的是为了简化Java栈的web开发。
Spring MVC的请求流程
Spring Web MVC 框架也是一个基于请求驱动的Web 框架，并且也使用了前端控制器模式来进行设计，再根据请求映射规则分发给相应的页面控制器（动作/处理器）进行处理。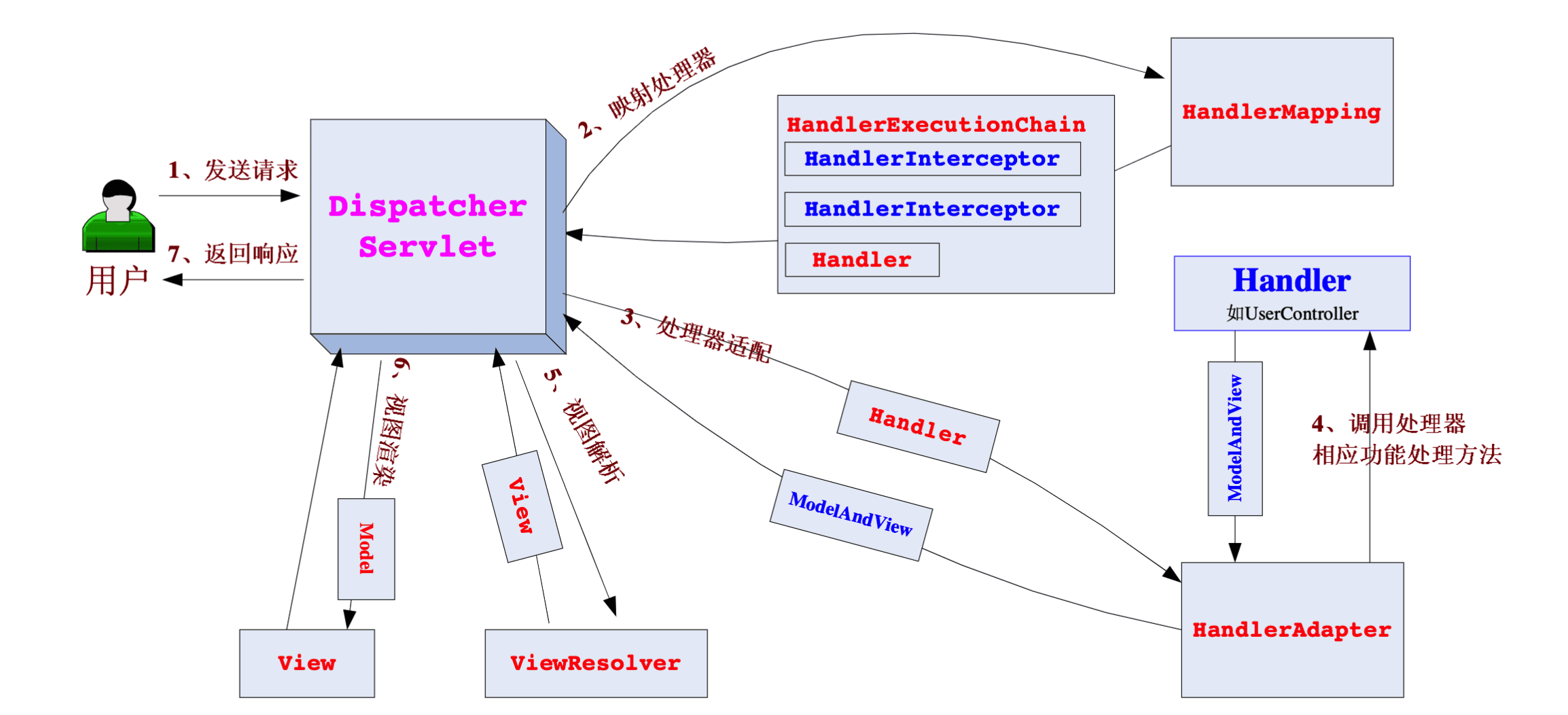
核心架构的具体流程步骤如下：
1、首先用户发送请求——>DispatcherServlet，前端控制器收到请求后自己不进行处理，而是委托给其他的解析器进行处理，作为统一访问点，进行全局的流程控制；
2、DispatcherServlet——>HandlerMapping， HandlerMapping 将会把请求映射为 HandlerExecutionChain 对象（包含一个Handler 处理器（页面控制器）对象、多个HandlerInterceptor 拦截器）对象，通过这种策略模式，很容易添加新的映射策略；
3、DispatcherServlet——>HandlerAdapter，HandlerAdapter 将会把处理器包装为适配器，从而支持多种类型的处理器，即适配器设计模式的应用，从而很容易支持很多类型的处理器；
4、HandlerAdapter——>处理器功能处理方法的调用，HandlerAdapter 将会根据适配的结果调用真正的处理器的功能处理方法，完成功能处理；并返回一个ModelAndView 对象（包含模型数据、逻辑视图名）；
5、ModelAndView 的逻辑视图名——> ViewResolver，ViewResolver 将把逻辑视图名解析为具体的View，通过这种策略模式，很容易更换其他视图技术；
6、View——>渲染，View 会根据传进来的Model 模型数据进行渲染，此处的Model 实际是一个Map 数据结构，因此很容易支持其他视图技术；
7、返回控制权给DispatcherServlet，由DispatcherServlet 返回响应给用户，到此一个流程结束。
补充：
1、Filter(ServletFilter)：进入Servlet前可以有preFilter, Servlet处理之后还可有postFilter
2、LocaleResolver：在视图解析/渲染时，还需要考虑国际化(Local)，显然这里需要有LocaleResolver.
3、ThemeResolver：如何控制视图样式呢？SpringMVC中还设计了ThemeSource接口和ThemeResolver，包含一些静态资源的集合(样式及图片等），用来控制应用的视觉风格。

拦截器

在Spring Boot中，你可以使用拦截器（Interceptor）来处理请求前、请求后或请求处理过程中的逻辑。拦截器通常用于执行一些跟请求处理相关的任务，例如身份验证、日志记录、权限检查等。以下是在Spring Boot中使用拦截器的基本步骤：

创建拦截器类：
首先，你需要创建一个Java类，实现HandlerInterceptor接口，该接口定义了拦截器的方法，包括preHandle、postHandle和afterCompletion等。这些方法分别用于在请求处理前、请求处理后和请求完成后执行相应的逻辑。

@Component
public class LoginTicketInterceptor implements HandlerInterceptor {
    // 登录信息拦截器（检查登录凭证是否有效）
    // 每次请求，不管是什么请求，都要检查登录信息；这在interceptor中完成，而不是在每个controller重写一遍
    @Autowired
    private UserService userService;
    @Autowired
    private HostHolder hostHolder;
    @Override
    public boolean preHandle(HttpServletRequest request, HttpServletResponse response, Object handler) throws Exception {
        String ticket = CookieUtil.getValue(request, "ticket");                 // 从cookie中获取凭证
        if (ticket != null) {
            LoginTicket loginTicket = userService.findLoginTicket(ticket);      // 查询凭证
            if (loginTicket != null && loginTicket.getStatus() == 0 && loginTicket.getExpired().after(new Date())) {      
                User user = userService.findUserById(loginTicket.getUserId());  // 若凭证有效，查询用户
                hostHolder.setUser(user);                                       // 在本次请求中持有用户
            }
        }
        return true;
    }
    @Override
    public void postHandle(HttpServletRequest request, HttpServletResponse response, Object handler, ModelAndView modelAndView) throws Exception {
        // 将登录用户的信息添加到ModelAndView对象中，这样在视图中可以方便地使用这些信息
        User user = hostHolder.getUser();
        if (user != null && modelAndView != null)  modelAndView.addObject("loginUser", user);
    }
    @Override
    public void afterCompletion(HttpServletRequest request, HttpServletResponse response, Object handler, Exception ex) throws Exception {
        // 清除hostHolder中持有的用户信息。确保每个请求处理完成后都不会泄漏用户信息或状态，以便下一个请求可以从头开始。
        hostHolder.clear();
    }
}

配置拦截器：
在Spring Boot应用程序中，通常在配置类中配置拦截器。你可以继承WebMvcConfigurerAdapter类（或实现WebMvcConfigurer接口）并覆盖addInterceptors方法，将你的拦截器添加到拦截器链中。

@Configuration
public class WebMvcConfig implements WebMvcConfigurer {
    @Autowired
    private LoginTicketInterceptor loginTicketInterceptor;
    @Override
    public void addInterceptors(InterceptorRegistry registry) {
        // 设置不拦截静态资源
        registry.addInterceptor(loginTicketInterceptor)
                .excludePathPatterns("/**/*.css", "/**/*.js", "/**/*.png", "/**/*.jpg", "/**/*.jpeg");
    }  }

Spring 事务管理

事务：是由N步数据库操作序列组成的逻辑扩行单元，这系列操作要么全执行，要么全放弃执行事务的特性(ACID)。报错会回滚。
常见的并发异常：第一类丢失更新、第二类丢失更新脏读、不可重复读、幻读。
事务隔离级别定义了多个并发事务之间的可见性和影响的程度。在关系型数据库中，常见的隔离级别包括：
DEFAULT：使用数据库的默认隔离级别。通常是READ_COMMITTED。
READ_UNCOMMITTED：允许一个事务读取另一个事务尚未提交的数据。最低的隔离级别，不推荐在生产环境中使用，因为可能会导致脏读、不可重复读和幻读问题。
READ_COMMITTED：保证一个事务不会读取到其他并发事务未提交的数据。这是大多数数据库的默认隔离级别。
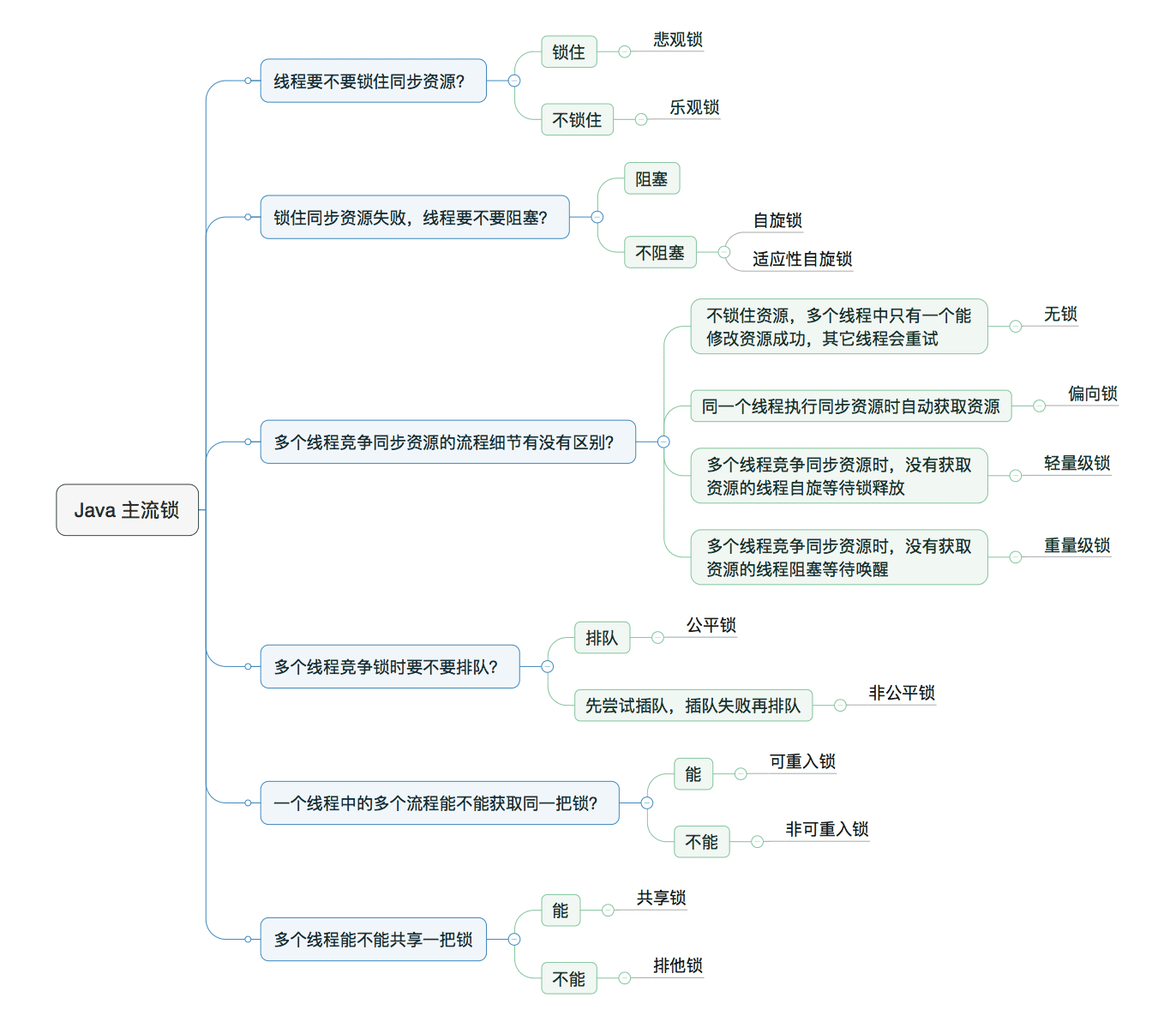
SERIALIZABLE：最高的隔离级别，确保事务串行执行，完全隔离了其他事务的影响。通常性能较差，不常用。
悲观锁 (数据库)
共享锁 (S锁)：事务A对某数据加了共享锁后，其他事务只能对该数据加共享锁，但不能加排他锁。
排他锁 (X锁)：事务A对某数据加了排他锁后，其他事对该数据既不能加共享锁，也不能加排他锁。
乐观锁(自定义)：版本号、时间戳等；若变化则取消本次更新，否则就更新数据(版本号+1)在更新数据前，检查版本号是否发生变
声明式事务：通过XML / 通过注解，声明某方法的事务特征。
通过 @Transactional(isolation = Isolation.READ_COMMITTED, propagation = Propagation.REQUIRED) 注解配置事务的属性，以控制事务的隔离级别（isolation）、传播行为（propagation）等。
常见的传播行为包括：REQUIRED, REQUIRES_NEW, SUPPORTS, NESTED
编程式事务：通过 TransactionTemplate 管理事务并通过它执行数据库的操作。（业务复杂/只处理其中几条代码时用）

统一异常处理

@ControllerAdvice：用于修饰类，表示该类是Controller的全局配置类（放在/controller/advice/下）；
在此类中，可以对Controller进行如下三种全局配置：异常处理方案、绑定数据方案、绑定参数方案
@ExceptionHandler：用于修饰（@ControllerAdvice所修饰类中的）方法，在Controller出现异常后被调用，用于处理捕获到的异常
@ModelAttribute：用于修饰方法，使其在Controller方法执行前被调用，用于为Model对象绑定参数（如获取从页面post的数据）

@DataBinder：用于修饰方法，该方法会在Controller方法执行前被调用，用于绑定参数的转换器

@ControllerAdvice(annotations = Controller.class)          // 表示扫描所有controller类
public class ExceptionAdvice {
    private static final Logger logger = LoggerFactory.getLogger(ExceptionAdvice.class);
    @ExceptionHandler({Exception.class})                   // 指处理所有类型的异常
    public void handleException(Exception e, HttpServletRequest request, HttpServletResponse response) throws IOException {
        logger.error("服务器发生异常: " + e.getMessage());  // 打印日志
        for (StackTraceElement element : e.getStackTrace()) {
            logger.error(element.toString()); }  }         // 打印具体报错

Spring Security

Spring Security是一个专注于为Java应用程序提供身份认证和授权的框架，它的强大之处在于它可以轻松扩展以满足自定义的需求
- 对身份的认证和授权提供全面的、可扩展的支持
- 防止各种攻击，如会话固定攻击、点击劫持、csrf攻击等
- 支持与Servlet API、Spring MVC等Web技术集成
核心概念：
- 认证（Authentication）：验证用户的身份。
- 授权（Authorization）：确定用户是否有权执行某个操作。
- 过滤器链（Filter Chain）：一系列的过滤器，用于处理认证和授权的请求。Spring Security的处理在 Spring MVC之前（ Security底层是基于filter，可以拦截大量请求）

基本配置：Spring Security 配置通常通过 Java 配置或 XML 配置完成。

@EnableWebSecurity   // Java 配置示例
public class SecurityConfig extends WebSecurityConfigurerAdapter {
    @Override
    protected void configure(HttpSecurity http) throws Exception {
        http
            .authorizeRequests()
                .antMatchers("/", "/home").permitAll()
                .anyRequest().authenticated()
                .and()
            .formLogin()
                .loginPage("/login")
                .permitAll()
                .and()
            .logout()
                .permitAll();
    }
    @Autowired
    public void configureGlobal(AuthenticationManagerBuilder auth) throws Exception {
        auth
            .inMemoryAuthentication()
                .withUser("user").password("{noop}password").roles("USER");
    }
}

安全过滤器链：Spring Security 的核心是安全过滤器链，它负责处理请求的认证和授权过程。在配置中，你可以通过 HttpSecurity 来定制过滤器链。

http
    .authorizeRequests()  // 对请求进行授权
        .antMatchers("/", "/home").permitAll()  // 允许所有用户访问
        .anyRequest().authenticated()  // 其他请求需要身份验证
        .and()
    .formLogin()  // 定义登录操作
        .loginPage("/login")  // 指定登录页
        .permitAll()
        .and()
    .logout()  // 定义登出操作
        .permitAll();

SecurityContext 是 Spring Security 中用于存储当前执行身份验证操作的上下文信息的接口。
它通常包含了与认证（Authentication）相关的信息，例如当前已认证的用户、用户的权限等。 SecurityContextHolder 负责管理 SecurityContext，而 SecurityContext 的实现则是 SecurityContextImpl。

// 在认证成功后，将认证对象放入 SecurityContext
UsernamePasswordAuthenticationToken authenticationToken = new UsernamePasswordAuthenticationToken(userDetails, null, userDetails.getAuthorities());
SecurityContext context = SecurityContextHolder.createEmptyContext();
context.setAuthentication(authenticationToken);
SecurityContextHolder.setContext(context);
// 在需要获取当前用户信息的地方
SecurityContext context = SecurityContextHolder.getContext();
Authentication authentication = context.getAuthentication();

2021-09-05

Java 并发

理论基础

多线程的出现是要解决什么问题的?

众所周知，CPU、内存、V0 设备的速度是有极大差异的，为了合理利用 CPU 的高性能，平衡这三者的速度差异，计算机体系结构、操作系统、编译程序都做出了贡献，主要体现为:
CPU 增加了缓存，以均衡与内存的速度差异; // 导致 可见性 问题
操作系统增加了进程、线程，以分时复用 CPU，进而均衡 CPU 与 I/0 设备的速度差异; // 导致 原子性 问题
编译程序优化指令执行次序，使得缓存能够得到更加合理地利用。 // 导致 有序性 问题

线程不安全是指什么?

如果多个线程对同一个共享数据进行访问而不采取同步操作的话，那么操作的结果是不一致的。

举例说明并发出现线程不安全的本质什么? 保障可见性，原子性和有序性。

可见性【CPU缓存引起】：一个线程对共享变量的修改，另外一个线程能够立刻看到。
原子性【分时复用引起】：即一个操作或者多个操作要么全部执行并且执行的过程不会被任何因素打断，要么就都不执行。
有序性【重排序引起】：即程序执行的顺序按照代码的先后顺序执行。

Java是怎么解决并发问题的? 3个关键字，JMM 和 8个 Happens-Before

Java 内存模型是个很复杂的规范，推荐：https://pdai.tech/md/java/jvm/java-jvm-jmm.html
理解的第一个维度：核心知识点
JMM本质上可以理解为，Java 内存模型规范了 JVM 如何提供按需禁用缓存和编译优化的方法。
具体来说，这些方法包括（1）volatile、synchronized 和 final 三个关键字；（2）Happens-Before
规则理解的第二个维度：可见性，有序性，原子性
- 原子性：在Java中，对基本数据类型的变量的读取和赋值操作是原子性操作，即这些操作是不可被中断的，要么执行要么不执行。（Java内存模型只保证了基本读取和赋值是原子性操作，如果要实现更大范围操作的原子性，可以通过synchronized和Lock来实现。由于synchronized和Lock能够保证任一时刻只有一个线程执行该代码块，那么自然就不存在原子性问题了，从而保证了原子性。）
- 可见性：Java提供了volatile关键字来保证可见性。当一个共享变量被volatile修饰时，它会保证修改的值会立即被更新到主存，当有其他线程需要读取时，它会去内存中读取新值。而普通的共享变量不能保证可见性，因为普通共享变量被修改之后，什么时候被写入主存是不确定的，当其他线程去读取时，此时内存中可能还是原来的旧值，因此无法保证可见性。（另外，通过synchronized和Lock也能够保证可见性，能保证同一时刻只有一个线程获取锁然后执行同步代码，并且在释放锁之前会将对变量的修改刷新到主存当中。因此可以保证可见性。）
- 有序性：通过volatile关键字来保证一定的“有序性”。另外可以通过synchronized和Lock来保证有序性，很显然，synchronized和Lock保证每个时刻是有一个线程执行同步代码，相当于是让线程顺序执行同步代码，自然就保证了有序性。当然JMM是通过Happens-Before 规则来保证有序性的。
关键字: volatile、synchronized 和 final
Happens-Before 规则：JVM 还规定了先行发生原则，让一个操作无需控制就能先于另一个操作完成。
- 1.单一线程原则Single Thread rule：在一个线程内，在程序前面的操作先行发生于后面的操作。
- 2.管程锁定规则Monitor Lock Rule：一个 unlock 操作先行发生于后面对同一个锁的 lock 操作。
- 3.??

线程安全是不是非真即假?…不是

一个类在可以被多个线程安全调用时就是线程安全的。
线程安全不是一个非真即假的命题，可以将共享数据按照安全程度的强弱顺序分成以下五类: 不可变、绝对线程安全、相对线程安全、线程兼容和线程对立。

不可变、
绝对线程安全、
相对线程安全、
线程兼容
线程对立。
，，

线程安全有哪些实现思路?

互斥同步
synchronized 和 ReentrantLock。
非阻塞同步
无同步方案
，，

如何理解并发和并行的区别?

并发：单核CPU宏观上可以处理多线程，是通过CPU调度实现的交替执行
并行：在多核CPU系统中利用每个处理器处理一个可以并发执行的程序，这样多个程序便可以同时执行。
上下文切换：线程上下文是指某一时间点 CPU寄存器和程序计数器的内容，CPU通过时间片分配算法来循环执行任务(线程)。多线程往往会比单线程更快更能够提高并发，但同时更多的线程意味着线程创建销毁开销加大、上下文非常频繁，程序反而不能支持更高的TPS。
时间片：时间片是CPU分配给各个任务(线程)的时间。多任务系统往往需要同时执行多道作业。作业数往往大于机器的CPU数，然而一颗CPU同时只能执行一项任务，利用了时间片轮转的方式进行调度。
建议：合理设置线程数目既可以最大化利用CPU，又可以减少线程切换的开销。高并发，低耗时的情况，建议少线程；低并发，高耗时的情况，建议多线程；高并发，高耗时的情况，要分析任务类型、增加排队、加大线程数

线程基础

进程、线程、纤程

Java 进程：在操作系统中，进程是基本的资源分配单位，操作系统通过进程来管理计算机的资源（指令加载到CPU、数据到内存、磁盘、网络，），每个进程有一个唯一的进程标识符(PID)用来区分。
当一个程序被运行，从磁盘加载这个程序的代码至内存，这时就开启了一个进程。进程就可以视为程序的一个实例。大部分程序可以同时运行多个实例进程（例如记事本、画图、浏览器等），也有的程序只能启动一个实例进程（例如网易云音乐、360 安全卫士等）
Java中，一个进程通常是指一个独立运行的 Java 虚拟机（JVM）实例；每个 Java 进程都有自己的内存空间、程序计数器、寄存器等资源，启动 Java 程序就启动了一个 Java 进程。
Java 线程：线程是操作系统中的基本执行单元(能够直接执行的最小代码块)，是CPU调度和分派的基本单位。一个进程可包含多个线程，每个线程独立执行不同的任务，共享进程的资源。一个线程就是一个指令流，将指令流中的一条条指令以一定的顺序交给 CPU 执行。同一时刻一个CPU核心只能运行一线程，8核CPU同时可以执行8个线程代码。
- Java 中，线程作为最小调度单位，进程作为资源分配的最小单位。
- 异步调用
  以调用方角度来讲，如果需要等待结果返回，才能继续运行就是同步；不需等待结果返回就能继续运行，是异步
  1. 设计：多线程可以让方法执行变为异步的（即不要巴巴干等着），比如说读取磁盘文件时，假设读取操作花费了 5 秒钟，如果没有线程调度机制，这 5 秒 cpu 什么都做不了，其它代码都得暂停…
  2. 结论：比如在项目中，视频文件需要转换格式等操作比较费时，这时开一个新线程处理视频转换，避免阻塞主线程tomcat 的异步 servlet 也是类似的目的，让用户线程处理耗时较长的操作，避免阻塞 tomcat 的工作线程ui 程序中，开线程进行其他操作，避免阻塞 ui 线程
- 效率提升
  1. 单核 cpu 下，多线程不能实际提高程序运行效率，只是为了能够在不同的任务之间切换，不同线程轮流使用cpu ，不至于一个线程总占用 cpu，别的线程没法干活
  2. 多核 cpu 可以并行跑多个线程，但能否提高程序运行效率还是要分情况的有些任务，经过精心设计，将任务拆分，并行执行，当然可以提高程序的运行效率。
  3. IO 操作不占用 cpu，只是我们一般拷贝文件使用的是【阻塞 IO】，这时相当于线程虽然不用 cpu，但需要一直等待 IO 结束，没能充分利用线程。所以才有后面的【非阻塞 IO】和【异步 IO】优化
- 进程与线程对比：
  进程基本上相互独立的，而线程存在于进程内，是进程的一个子集
  进程拥有共享的资源，如内存空间等，供其内部的线程共享
  进程间通信较为复杂，同一台计算机的进程通信称为 IPC（Inter-process communication）；不同计算机之间的进程通信，需要通过网络，并遵守共同的协议，例如 HTTP
  线程通信相对简单，因为它们共享进程内的内存，一个例子是多个线程可以访问同一个共享变量
  线程更轻量，线程上下文切换成本一般上要比进程上下文切换低
纤程：Java19才支持虚拟线程(纤程【协程】)
- 纤程可以在一个线程内部创建多个纤程这些纤程之间可以共享同一个线程的资源
- 纤程是在同一个进程内部运行的，不需操作系统的介入，可以在用户空间内实现协作式多任务处理（jvm级别的）。因此纤程的创建和销毁开销很小，可更高效地利用系统资源。
- 先有进程，然后进程可以创建线程，线程是依附在进程里面的。
  线程里面可以包含多个协程；进程之间不共亭全局变量。线程之间共享全局变量，但是要注意资源竞争的问题
常用方法
- start() 与 run()
  - 类型：run方法是同步方法（按代码顺序执行），而start方法是异步方法（创建新线程，进入就绪状态，等待OS调用）
  - 作用：run方法的作用是存放（执行）任务代码，不产生新线程；而start方法创建，启动一个新线程，并调用其 run方法
  - 执行次数：run方法可以被执行无数次，而start方法只能被执行一次，原因在于线程不能被重复启动
- setName()：给当前线程取名字
- getName()：获取当前线程的名字。线程存在默认名称：子线程是 Thread-索引，主线程是 main
- sleep()：让当前线程休眠多少毫秒再继续执行，Thread.sleep(0):让操作系统立刻重新进行一次cpu竞争。
  - 调用 sleep 会让当前线程从 Running 进入 Timed Waiting 状态（阻塞）；睡眠结束后的线程未必会立刻得到执行
  - 可以使用 interrupt() 打断正在睡眠的线程，这时 sleep() 会抛出 InterruptedException.
  - 建议用 TimeUnit的 sleep() 代替 Thread 的 sleep 来获得更好的可读性，其底层还是 sleep 方法.
  - 在循环访问锁的过程中，可以加入sleep让线程阻塞时间，防止大量占用cpu资源其它线程。
- yield()：提示线程调度器尽力让出当前线程对CPU的使用，让当前线程从 Running？？进入 Runnable 就绪状态
- setPriority()：更改该线程的优先级，1~10，(CPU忙时)优先级越大被CPU调度的几率越高。
- getPriority()：返回该线程的优先级
- isInterrupted()：判断是否打断，不会清楚打断标记
- interrupt()：中断这个线程，异常处理机制。实际上，并不会直接中断线程的执行，只是设置线程的中断标记，线程可以在适当的时候检查这个标记并自行决定中断执行。
  - 打断 sleep，wait，join 的线程，会清空打断状态
  - 打断正常运行的线程，不会清空打断状态
- join()：主线程将等待这个线程结束再顺序执行代码（异步变同步了），可以设置等待millis毫秒。
- setDaemon(true)：设置守护线程；可以通过 Thread.isDaemon()来判断
  - 默认情况下创建的线程都是用户线程(普通线程)，需要等待所有的线程执行完毕后，进程才会结束
  - 当所有的用户线程退出后，守护线程会立马结束
  - 应用：垃圾回收器线程属于守护线程，tomcat用来接受处理外部的请求的线程就是守护线程

线程有哪几种状态? 分别说明从一种状态到另一种状态转变有哪些方式?

Java 中线程状态是用 6个enum 表示
- NEW：初始状态，线程被构建，但是还没有调用start()
- RUNNABLE：可能正在运行（运行状态），也可能正在等待 CPU 时间片（可运行状态）（，还可能处在OS层面的阻塞状态，如正在进行IO操作）。Java线程将操作系统中的就绪和运行两种状态统称为“运行中”。
- BLOCKED：阻塞状态，表示线程阻塞于锁。等待获取一个排它锁，如果其线程释放了锁就会结束此状态。
- WAITING：无限期等待，等待其它线程显式地唤醒，否则不会被分配 CPU 时间片。如，等待一个死循环 t.join()，当前线程将无限期等待。
- TIME_WAITING：限期等待，无需等待其它线程显式地唤醒，在一定时间之后会被系统自动唤醒。
  调用 Thread.sleep() 方法使线程进入限期等待状态时，常常用“使一个线程睡眠”进行描述。调用 Object.wait() 方法使线程进入限期等待或者无限期等待时，常常用“挂起一个线程”进行描述。
  ？？睡眠和挂起是用来描述行为，而阻塞和等待用来描述状态。阻塞和等待的区别在于，阻塞是被动的，它是在等待获取一个排它锁。而等待是主动的，通过调用 Thread.sleep() 和 Object.wait() 等方法进入。
- TERMINATED：终止状态。可以是线程结束任务之后自己结束，或者产生了异常而结束。

通常线程有哪几种使用方式?

有三种使用线程的方法：实现 Runnable 接口，实现 Callable 接口，继承 Thread 类。
实现 Runnable 和 Callable 接口的类只能当做一个可以在线程中运行的任务，不是真正意义上的线程，因此最后还需要通过 Thread 来调用。可以说任务是通过线程驱动从而执行的。
实现接口 VS 继承 Thread：实现接口会更好一些。因为 Java 不支持多重继承，因此继承了 Thread 类就无法继承其它类，但是可以实现多个接口；类可能只要求可执行就行，继承整个 Thread 类开销过大。

通过继承Thread类，重写run方法。
Thread 类也实现了 Runable 接口。当调用 start() 方法启动一个线程时，虚拟机会将该线程放入就绪队列中等待被调度，当一个线程被调度时会执行该线程的 run() 方法。

public class MyThread extend Thread {
    @Override
    public void run() { ...}
}

public static void main(String[] args) {
    // 启动过程为: thread.start()->中间过程->thread.run() 即重写的方法
    MyThread mt = new MyThread();
    // 开启异步线程：异步，创建一个新线程 mt
    mt.start();
}

通过实现Runnable接口：
需要实现 run() 方法。通过 Thread 调用 start() 方法来启动线程。
通过 Runnable接口把线程和任务分开了；用 Runnable 更容易与线程池等高级 API 配合；用 Runnable 让任务类脱离了 Thread 继承体系，更灵活

public class MyRunnable implements Runnable {
    @Override
    public void run() { ...}
}

public static void main(String[] args) {
    // 通过实现Runnable接口。实例化Thread，传递一个Runable任务
    // 启动过程为: thread.start()->中间过程>thread.run() 默认逻辑->runable.run() 实际业务
    Thread thread = new Thread(new MyRunnable());
    thread.start();
}
// 主线程main、线程thread 异步执行

实现 Callable 接口：
与 Runnable 相比，Callable 可以有返回值，返回值通过 FutureTask 进行封装。

1
2
3

public class MyCallable implements Callable<Integer> {
    public Integer call() { ...}
}

public static void main(String[] args) throws ExecutionException, InterruptedException {
    MyCallable mc = new MyCallable();
    FutureTask<Integer> ft = new FutureTask<>(mc);
    Thread thread = new Thread(ft);
    thread.start();
    System.out.println(ft.get());
}

基础线程机制有哪些?

Executor：管理多个异步任务的执行，而无需程序员显式地管理线程的生命周期。
这里的异步是指多个任务的执行互不干扰，不需要进行同步操作。主要有三种 Executor:
- CachedThreadPool: 一个任务创建一个线程；
- FixedThreadPool: 所有任务只能使用固定大小的线程；
- SingleThreadExecutor: 相当于大小为 1 的 FixedThreadPool。

public static void main(String[] args) {
    ExecutorService executorService = Executors.newCachedThreadPool();
    for (int i = 0; i < 5; i++) {
        executorService.execute(new MyRunnable());
    }
    executorService.shutdown();
}

Daemon：守护线程，是程序运行时在后台提供服务的线程，不属于程序中不可或缺的部分。
当所有非守护线程结束时，程序也就终止，同时会杀死所有守护线程。main() 属于非守护线程。使用 setDaemon() 方法将一个线程设置为守护线程。
1
2
3
4
public static void main(String[] args) {
Thread thread = new Thread(new MyRunnable());
thread.setDaemon(true);
}

线程的中断方式有哪些?

一个线程执行完毕之后会自动结束，如果在运行过程中发生异常也会提前结束。

InterruptedException：通过调用一个线程的 interrupt() 来中断该线程，如果该线程处于阻塞、限期等待或者无限期等待状态，那么就会抛出 InterruptedException，从而提前结束该线程。但是不能中断 I/O 阻塞和 synchronized 锁阻塞。
interrupted()：如果一个线程的 run() 方法执行一个无限循环，并且没有执行 sleep() 等会抛出 InterruptedException 的操作，那么调用线程的 interrupt() 方法就无法使线程提前结束。
但是调用 interrupt() 方法会设置线程的中断标记，此时调用 interrupted() 方法会返回 true。因此可以在循环体中使用 interrupted() 方法来判断线程是否处于中断状态，从而提前结束线程。
Executor 的中断操作：调用 Executor 的 shutdown() 方法会等待线程都执行完毕之后再关闭，但是如果调用的是 shutdownNow() 方法，则相当于调用每个线程的 interrupt() 方法。
？？？
过时方法：stop(), suspend()休眠, resume()？？

线程的互斥同步方式有哪些? 如何比较和选择?

Java 提供两种锁机制来控制多个线程对共享资源的互斥访问：JVM 实现的 synchronized，JDK 实现的 ReentrantLock
???
https://pdai.tech/md/java/thread/java-thread-x-thread-basic.html#%E7%BA%BF%E7%A8%8B%E4%BA%92%E6%96%A5%E5%90%8C%E6%AD%A5

线程之间有哪些协作方式?

当多个线程可以一起工作去解决某个问题时，如果某些部分必须在其它部分之前完成，那么就需要对线程进行协调。

join()：在线程中调用另一个线程的 join() 方法，会将当前线程挂起，而不是忙等待，直到目标线程结束。
对于以下代码，虽然 b 线程先启动，但是因为在 b 线程中调用了 a 线程的 join() 方法，b 线程会等待 a 线程结束才继续执行，因此最后能够保证 a 线程的输出先于 b 线程的输出。
wait()，notify()，notifyAll()
调用 wait() 使得线程等待某个条件满足，线程在等待时会被挂起，当其他线程的运行使得这个条件满足时，其它线程会调用 notify() 或者 notifyAll() 来唤醒挂起的线程。它们都属于 Object 的一部分，而不属于 Thread。只能用在同步方法或者同步控制块中使用，否则会在运行时抛出 IllegalMonitorStateExeception。使用 wait() 挂起期间，线程会释放锁。这是因为，如果没有释放锁，那么其它线程就无法进入对象的同步方法或者同步控制块中，那么就无法执行 notify() 或者 notifyAll() 来唤醒挂起的线程，造成死锁。
await()，signal()，signalAll()
java.util.concurrent 类库中提供了 Condition 类来实现线程之间的协调，可以在 Condition 上调用 await() 方法使线程等待，其它线程调用 signal() 或 signalAll() 方法唤醒等待的线程。相比于 wait() 这种等待方式，await() 可以指定等待的条件，因此更加灵活。

Java锁

Java提供了种类丰富的锁，每种锁因其特性的不同，在适当的场景下能够展现出非常高的效率。

乐观锁 VS 悲观锁
乐观锁与悲观锁是一种广义上的概念，体现了看待线程同步的不同角度。Java和数据库中都有此概念对应的实际应用。
- 对于同一个数据的并发操作，悲观锁认为自己在使用数据的时候一定有别的线程来修改数据，因此在获取数据的时候会先加锁，确保数据不会被别的线程修改。Java中，synchronized关键字和Lock的实现类都是悲观锁。
- 乐观锁认为自己在使用数据时不会有别的线程修改数据，所以不会添加锁，只是在更新数据的时候去判断之前有没有别的线程更新了这个数据。如果数据没有被更新，当前线程将自己修改的数据成功写入；如果数据已经被其他线程更新，则根据不同的实现方式执行不同的操作（例如报错或者自动重试）。
  乐观锁在Java中是通过使用无锁编程来实现，最常用的是CAS算法，Java原子类中的递增操作就通过CAS自旋实现的。
- 悲观锁适合写操作多的场景，先加锁可以保证写操作时数据正确。
  乐观锁适合读操作多的场景，不加锁的特点能够使其读操作的性能大幅提升。
独享锁(排他锁) VS 共享锁
- 独享锁也叫排他锁（写锁），指该锁一次只能被一个线程所持有。如果线程T对数据A加上排它锁后，则其他线程不能再对A加任何类型的锁。获得排它锁的线程即能读数据又能修改数据。JDK中的synchronized和JUC中Lock的实现类就是互斥锁。
- 共享锁（读锁）是指该锁可被多个线程所持有。如果线程T对数据A加上共享锁后，则其他线程只能对A再加共享锁，不能加排它锁。获得共享锁的线程只能读数据，不能修改数据。

CAS

不加锁的情况下保持数据读写一致。
CAS在java中的底层实现： lockcmpxchg

对象的内存布局？？

对象头、类型指针、实例数据、对齐

共享模型之管程

一个程序运行多个线程本身是没有问题的，问题出在多个线程访问共享资源；多个线程读共享资源其实也没有问题，在多个线程对共享资源读写操作时发生指令交错，就会出现问题。
一段代码块内如果存在对共享资源的多线程读写操作，称这段代码块为临界区。多个线程在临界区内执行，由于代码的执行序列不同而导致结果无法预测，称之为发生了竞态条件。
为了避免临界区的竞态条件发生，有多种手段可以达到目的。阻塞式的解决方案：synchronized，Lock；非阻塞式的解决方案：原子变量。

synchronized 解决方案

synchronized，即俗称的【对象锁】，它采用互斥的方式让同一时刻至多只有一个线程能持有【对象锁】，其它线程再想获取这个【对象锁】时就会阻塞住。
synchronized 实际是用对象锁保证了临界区内代码的原子性，临界区内的代码对外是不可分割的，拥有锁的线程可以安全的执行临界区内的代码，不会被线程切换所打断。临界区中的代码只能被串行运行。

static int counter = 0;
// 同一时刻 t1，t2 中只有其一能持有对象锁 room 以执行临界区中的代码
static final Object room = new Object(); 
Thread t1 = new Thread(() -> {
    for (int i = 0; i < 5000; i++) {
        // 当线程 t1 执行到 synchronized(room) 时持有了对象锁，执行 count++ 代码
        // 这中间即使 t1 的 cpu 时间片不幸用完，其仍将持有对象锁
        synchronized (room) {
            counter++;  // 获取了对象锁后，自增的四个原子操作便作为一个整体，不可打断
        }
    }
}, "t1");

Thread t2 = new Thread(() -> {
    for (int i = 0; i < 5000; i++) {
        // 如果 t2 运行到 synchronized(room) 时 t1 仍持有对象锁，t2 将发生上下文切换，阻塞
        // 当 t1 执行完 synchronized{} 块内的代码，这时才释放对象锁，唤醒 t2 线程并让 t2 持有锁
        synchronized (room) {
            counter--;
        }
    }
}, "t2");

面向对象改进

class Room {
    // 需要保护的共享变量作为类的成员变量
    int value = 0;
    public void increment() {
        // 自身实例化的对象作为锁
        synchronized (this) {
            value++;
        }
    }
    public void decrement() {
        synchronized (this) {
            value--;
        }
    }
    public int get() {
        synchronized (this) {
            return value;
        }
    }
}

方法上的 synchronized

class Test{
    public synchronized void test() {
        // 在这个方法内，只有一个线程能够访问 Resource
        Resource++;
    }
}
// 等价于代码块级别的：
class Test{
    public void test() {
        // 该实例化对象作为锁
        synchronized(this) {
            Resource++;
        }
    }
}

静态方法上的 synchronized

class Test{
    public synchronized static void test() {
    }
}
// 等价于
class Test{
    public static void test() {
        // 该类作为锁
        synchronized(Test.class) {

        }
    }
}

所谓的“线程八锁”
,,,

线程安全分析

成员变量和静态变量是否线程安全？
- 如果它们没有共享，则线程安全；
- 如果它们被共享了，根据它们的状态是否能够改变，又分两种情况：
  - 如果只有读操作，则线程安全
  - 如果有读写操作，则这段代码是临界区，需要考虑线程安全
局部变量是否线程安全？
- 局部变量是线程安全的
  线程调用方法时局部变量 i，会在每个线程的栈帧内存中被创建多份（线程私有局部变量表），因此不存在共享
- 但局部变量引用的对象则未必：如果该对象没有逃离方法的作用访问，它是线程安全的；如果该对象逃离方法的作用范围，需要考虑线程安全
常见线程安全类
String、Integer、StringBuffer、Random、Vector、Hashtable、java.util.concurrent 包下的类
这里说它们是线程安全的是指，多个线程调用它们同一个实例的某个方法时，是线程安全的。它们的每个方法是原子的，但注意它们多个方法的组合不是原子的！！
1
2
3
4
5
// 下面代码是否线程安全？不安全
Hashtable table = new Hashtable();
if( table.get("key") == null) {
table.put("key", value);
}
不可变类线程安全性
String、Integer 等都是不可变类，因为其内部的状态不可以改变，因此它们的方法都是线程安全的
String 有 replace，substring 等方法【可以】改变值啊，那么这些方法又是如何保证线程安全的呢？生成并且指向新的类。
实例分析
https://www.bilibili.com/video/BV16J411h7Rd?p=69&vd_source=ff210768dfaee27c0d74f9c8c50d7274
例题
https://www.bilibili.com/video/BV16J411h7Rd?p=69&vd_source=ff210768dfaee27c0d74f9c8c50d7274

Monitor

，，

wait/notify

，，

线程状态转换

，，

活跃性

，，

Lock

，，

非共享模型

，，

JUC 类汇总

JUC是 java.util.concurrent包的缩写，说白了就是并发场景进行多线程编程的工具类。
总的来说就是在并发场景下，怎么让程序尽量通过有限的硬件，高效的处理请求，并且保证程序“线程安全”。
开发高并发、高性能系统（1）加快响应用户的时间（2）使代码模块化、异步化、简单化（3）充分利用CPU的多核资源

Java 线程池？？

JDK 线程池
- ExecutorService
- ScheduledExecutorService（定时任务）
Spring 线程池
- ThreadPoolTaskExecutor
- ThreadPoolTaskScheduler（定时任务）
分布式定时任务
- Spring Quartz：不同服务器上的quartz线程依赖于同一个数据库

// JDK普通线程池
private ExecutorService executorService = Executors.newFixedThreadPool(5);
// JDK可执行定时任务的线程池
private ScheduledExecutorService scheduedExecutorSevice = Executors.newScheduledThreadPool(5);
// Spring普通线程池
@Autowired
private ThreadPoolTaskExecutor taskExecutor;
// Spring可执行定时任务的线程池
@Autowired
private ThreadPoolTaskScheduler taskScheduler;

// 在 AlphaService 中给方法加上 @Async，使该方法在多线程环境下被异步的调用（被主线程并发并发，异步执行）
// 在 AlphaService 中给方法加上 @Scheduled，只要有程序再跑就会自动调用
@Autowired
private AlphaService alphaService;

// 1.JDK普通线程池
public void testExecutorService() {
    Runnable task = new Runnable() {};
    for (int i = 0; i < 10; i++) {
        executorService.submit(task);
    }
}
// 2.JDK定时任务线程池
public void testScheduledExecutorService() {
    Runnable task = new Runnable() {};
    scheduledExecutorService.scheduleAtFixedRate(task, 10000, 1000, TimeUnit.MILLISECONDS);
}
// 3.Spring普通线程池
public void testThreadPoolTaskExecutor() {
    Runnable task = new Runnable() {};
    for (int i = 0; i < 10; i++) {
        taskExecutor.submit(task);
    }
}
// 4.Spring定时任务线程池
public void testThreadPoolTaskScheduler() {
    Runnable task = new Runnable() {};
    Date startTime = new Date(System.currentTimeMillis() + 10000);
    taskScheduler.scheduleAtFixedRate(task, startTime, 1000);
}
// 5.Spring普通线程池(简化)
public void testThreadPoolTaskExecutorSimple() {
    for (int i = 0; i < 10; i++) {
        // 并发，异步执行 AlphaService 中的 加了@Async 的 execute1()
        alphaService.execute1();
    }
}
// 6.Spring定时任务线程池(简化)
public void testThreadPoolTaskSchedulerSimple() {
    // 自动调用 AlphaService 中的加上 @Scheduled 的方法
}

2021-09-04

JVM

JVM (Java虚拟机)本质上是一个计算机程序，他的职责是运行 Java字节码文件，解释为对应OS的机器指令。
JVM 包含内存管理、解释执行虚拟机指令、即时编译三大功能。
常见的JVM有HotSpot、GraalVM、OpenJ9等，另外DragonWell龙井JDK也提供了一款功能增强版的JVM。其中使用最广泛的是HotSpot。

JVM 跨平台原理

本质是不同操作系统上提供了不同的JVM。（下载JDK/JRE for Linux/Windows…）
Java 代码“一次编写，到处执行”，其实是指由.java文件编译来的.class字节码文件（高级语言java –> javac编译 –> 字节码(提升程序运行的效率，跨平台运行)）能够通过不同操作系统上的 JVM 解释为该操作系统的机器指令。
JVM 也不再只支持Java，由此衍生出了许多基于JVM的编程语言，如Groovy, Scala, Koltin等等。

JVM 知识要点

1. 类加载器：将class字节码文件中的内容加载到内存中。 2. 运行时数据区域：负责管理JVM 使用到的内存，比如创建对象和销毁对象。 3. 执行引擎：将字节码文件中的指令解释成机器码，同时使用即时编译器优化性能，用gc回收内存。 4. 本地接口：调用本地已经编译好的方法（不在字节码文件中）比如虚拟机中提供的cpp方法。

类的生命周期

类的生命周期：加载，连接，初始化，使用，卸载
其中类加载的过程包括了加载、验证、准备、解析、初始化五个阶段。
在这五个阶段中，加载、验证、准备和初始化这四个阶段发生的顺序是确定的，而解析阶段则不一定，它在某些情况下可以在初始化阶段之后开始，这是为了支持Java语言的运行时绑定(也成为动态绑定或晚期绑定)。另外注意这里的几个阶段是按顺序开始，而不是按顺序进行或完成，因为这些阶段通常都是互相交叉地混合进行的，通常在一个阶段执行的过程中调用或激活另一个阶段。

类的加载：查找并加载类的二进制数据
- 类加载器通过一个类的全限定名来获取其定义的二进制字节流。可以使用Java代码拓展的不同的渠道。
- JVM 将字节码中的信息保存到内存的方法区（虚拟概念）
- 生成一个InstanceKlass对象（c++编写），保存类的所有信息，里边还包含实现特定功能比如多态的信息。
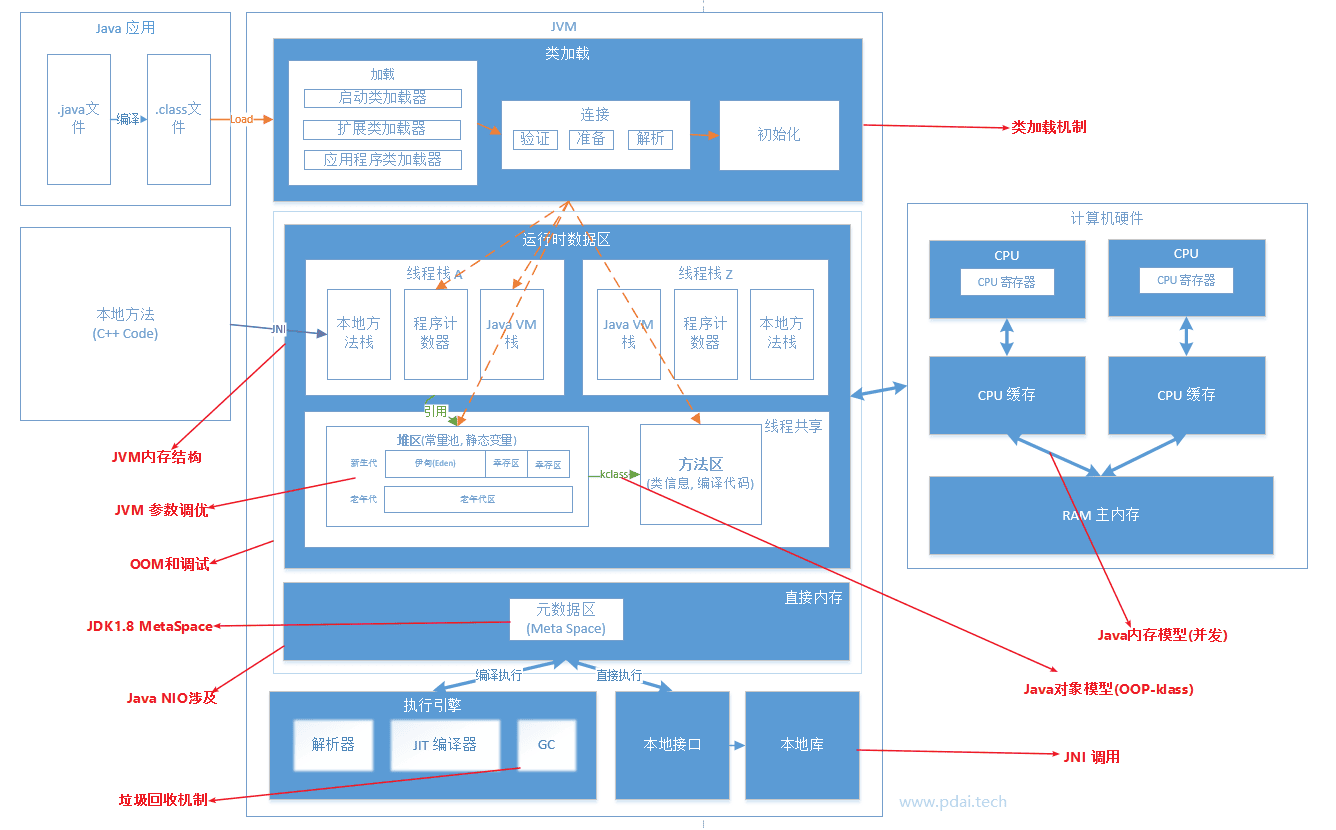
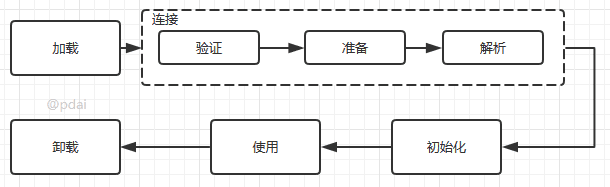
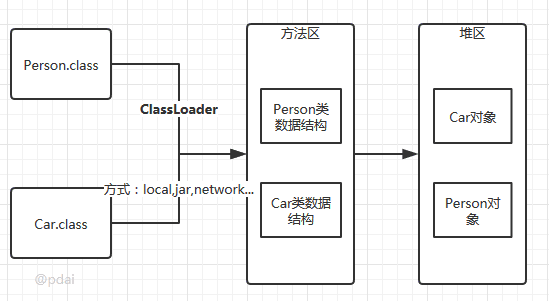- 在Java堆中生成一个代表这个类的java.lang.Class对象（包含字段比InstanceKlass中的少，控制访问范围和保证安全性），作用是在Java代码中去获取类的信息（反射），以及存储静态字段的数据（JDK8后）加载阶段完成后，虚拟机外部的二进制字节流就按照虚拟机所需的格式存储在方法区之中，而且在Java堆中也创建一个java.lang.Class类的对象，这样便可以通过该对象访问方法区中的这些数据。类加载器并不需要等到某个类被“首次主动使用”时再加载它，JVM规范允许类加载器在预料某个类将要被使用时就预先加载它，如果在预先加载的过程中遇到了.class文件缺失或存在错误，类加载器必须在程序首次主动使用该类时才报告错误(LinkageError错误)如果这个类一直没有被程序主动使用，那么类加载器就不会报告错误。
- 加载.class文件的方式：从本地系统中直接加载、通过网络下载.class文件、从zip，jar等归档文件中加载.class文件、从专有数据库中提取.class文件、将Java源文件动态编译为.class文件
连接
- 2.1 验证: 确保被加载的类的正确性。验证是连接阶段的第一步，这一阶段的目的是为了确保Class文件的字节流中包含的信息符合当前虚拟机的要求，并且不会危害虚拟机自身的安全。
  - 文件格式验证: 验证字节流是否符合Class文件格式的规范；例如: 是否以0xCAFEBABE开头、主次版本号是否在当前虚拟机的处理范围之内（不能高于环境jdk版本）、常量池中的常量是否有不被支持的类型。
  - 元数据验证: 对字节码描述的信息进行语义分析(注意: 对比javac编译阶段的语义分析)，以保证其描述的信息符合Java语言规范的要求；例如: 这个类是否有父类，除了java.lang.Object之外。
  - 字节码验证: 通过数据流和控制流分析，确定程序语义是合法的、符合逻辑的。
  - 符号引用验证: 确保解析动作能正确执行。
- 2.2 准备: 为类的静态变量分配内存，并将其初始化为默认值。这些内存都将在方法区中分配。
  - 这时进行内存分配的仅包括类变量(static)，而不包括实例变量，实例变量在对象实例化时随着对象一块分配在Java堆
  - 这里所设置的初始值通常情况下是数据类型默认的零值(如0、0L、null、false等)，而不是被在Java代码中被显式地赋予的值。假设一个类变量的定义为: public static int value = 3；那么变量value在准备阶段过后的初始值为0，而非3，因为这时候尚未开始执行任何Java方法，把value赋值为3的动作将在初始化阶段才会执行。
  - 对于同时被static和final修饰的常量，必须在声明的时候就为其显式地赋值，否则编译时不通过；而只被final修饰的常量则既可以在声明时显式地为其赋值，也可以在类初始化时显式地为其赋值，系统不会为其赋予默认零值。
  - 对基本数据类型来说，对于类变量(static)和全局变量，如果不显式地对其赋值而直接使用，则系统会为其赋予默认的零值.而局部变量使用前必须显式地为其赋值，否则编译时不通过。
  - 对于引用数据类型reference来说，如数组引用、对象引用等，如果没有对其进行显式地赋值而直接使用，系统都会为其赋予默认的零值，即null。
- 2.3 解析: 把类中的符号引用（在字节码文件中使用编号来访问常量池中内容）转换为直接引用（符号->内存地址）
  解析阶段是虚拟机将常量池内的符号引用替换为直接引用的过程，解析动作主要针对类或接口、字段、类方法、接口方法、方法类型、方法句柄和调用点限定符7类符号引用进行。符号引用就是一组符号来描述目标，可以是任何字面量。直接引用就是直接指向目标的指针、相对偏移量或一个间接定位到目标的句柄。
初始化：为类的静态变量赋予正确的初始值，JVM负责对类进行初始化，主要对类变量进行初始化。
- 在Java中对类变量进行初始值设定有两种方式: 声明类变量是指定初始值、使用静态代码块为类变量指定初始值
- JVM初始化步骤
  - 假如这个类还没有被加载和连接，则程序先加载并连接该类
  - 假如该类的直接父类还没有被初始化，则先初始化其直接父类
  - 假如类中有初始化语句，则系统依次执行这些初始化语句
- 类初始化时机: 只有当对类的主动使用的时候才会导致类的初始化，类的主动使用包括以下:
  - 创建类的实例，也就是new的方式
  - 访问某个类或接口的静态变量（注意final修饰且等号右边是常量的变量不会触发初始化）或者对该静态变量赋值
  - 调用类的静态方法、执行Main方法的当前类
  - 反射(如Class.forName(“com.pdai.jvm.Test”))
  - 初始化某个类的子类，则其父类也会被初始化
  - Java虚拟机启动时被标明为启动类的类(Java Test)，直接使用java.exe命令来运行某个主类
使用
（即程序员工作阶段）类访问方法区内的数据结构的接口，对象是Heap区的数据。
卸载
- Java虚拟机将结束生命周期的几种情况：
  - 执行了System.exit()方法
  - 程序正常执行结束
  - 程序在执行过程中遇到了异常或错误而异常终止
  - 由于操作系统出现错误而导致Java虚拟机进程终止

JVM 类加载

【 类的生命周期的加载，连接，初始化阶段 】

类字节码详解

源代码通过编译器编译为字节码，再通过类加载子系统进行加载到JVM中运行；
字节码文件中保存了源代码编译之后的内容，以二进制的方式存储，无法直接用记事本打开阅读；
常用工具：对于本地/服务器上的字节码文件：javap；jclasslib，有idea插件版本，在代码编译（构建项目）后实时看到字节码文件内容。
对于运行中的程序：Arthas 是一款线上监控诊断产品，通过全局视角实时查看应用load、内存、gc、线程的状态信息，并能在不修改应用代码的情况下，对业务问题进行诊断，大大提升线上问题排查效率。（jar包，使用java -jar启动 Arthas包）服务器上文件使用javap命令直接查看，也可以通过arthas的dump命令导出字节码文件再查看本地文件。还可以使用jad命令反编译出源代码。

基础信息：magic魔数（Java文件头 CAFEBABE，软件通过文件头来校验文件的类型，而非文件扩展名），主副版本号（指编译字节码文件的JDK版本号(如主版本号52对应JDK8，减44) 用于判断当前字节码的版本与运行时的JDK是否兼容(低版本JDK不能运行高版本字节码)冲突时建议降低第三方依赖的版本号），访问标识（public，final等等），父类和接口
常量池：避免相同内容重复定义，节省空间。保存了字符串常量、类或接口名、字段名主要在字节码指令中使用。
常量池中的数据都有一个编号，编号从1开始。在字段或者字节码指令中通过编号可以快速的找到对应的数据。
字节码指令中通过编号引用到常量池的过程称之为符号引用。
字段：当前类或接口声明的字段信息
方法：当前类或接口声明的方法信息，为字节码指令（在操作数栈和局部变量表上执行 iconst，istore，iload，iinc等指令，i++和++i区别就在指令iinc和iload的顺序颠倒）
main方法：Java类的main方法是程序的入口点。在字节码文件中，这通常表示为public static void main(String[] args)方法。Java虚拟机（JVM）将通过public static void main(String[] args)方法来执行程序。字节码指令会调用这个方法，并它将启动程序的执行。
init方法：类的构造函数，用于创建类的实例。在字节码文件中，方法是类的构造函数，用于初始化新对象的状态。这个方法通常是由invokespecial指令调用的，用于初始化新对象。
clinit方法：类的类构造函数，也称为静态初始化方法。这个方法用于执行类的静态初始化代码块。在字节码文件中，方法通常由clinit指令表示。这个方法用于执行类级别的静态初始化操作
Code属性：每个方法都有一个Code属性，其中包含了该方法的字节码指令，也就是方法体的实际执行代码
属性：类的属性，比如源码的文件名，内部类的列表等

类加载器

类加载器(ClassLoader)负责在类加载过程中的字节码获取并加载到内存这一部分。通过加载字节码数据放入内存转换成byte[]（只负责这一部分），接下来调用虚拟机底层方法将byte[]转换成方法区和堆中的数据。
站在Java开发人员的角度来看，类加载器可以大致划分为以下三类：

启动类加载器: Bootstrap ClassLoader，负责加载存放在JDK\jre\lib(JDK代表JDK的安装目录，下同)下，或被-Xbootclasspath参数指定的路径中的，并且能被虚拟机识别的类库(如rt.jar，所有的java.*开头的类均被Bootstrap ClassLoader加载)。启动类加载器是无法被Java程序直接引用的，无法直接通过代码查看，程序员难以直接调试。
它使用C++实现(这里仅限于Hotspot，也就是JDK1.5之后默认的虚拟机，有很多其他的虚拟机是用Java语言实现的)，是虚拟机自身的一部分；所有其他的类加载器都由Java语言实现，独立于虚拟机之外，并且全部继承自抽象类java.lang.ClassLoader，这些类加载器需要由启动类加载器加载到内存中之后才能去加载其他的类。
扩展类加载器: Extension ClassLoader，该加载器由sun.misc.Launcher$ExtClassLoader实现，它负责加载JDK\jre\lib\ext目录中，或者由java.ext.dirs系统变量指定的路径中的所有类库(如javax.*开头的类)，开发者可以直接使用扩展类加载器。
应用程序类加载器: Application ClassLoader，该类加载器由sun.misc.Launcher$AppClassLoader来实现，它负责加载用户类路径(ClassPath)所指定的类，开发者可以直接使用该类加载器，如果应用程序中没有自定义过自己的类加载器，一般情况下这个就是程序中默认的类加载器。

应用程序都是由这三种类加载器互相配合进行加载的，如果有必要，我们还可以加入自定义的类加载器。
因为JVM自带的ClassLoader只是懂得从本地文件系统加载标准的java class文件，因此如果编写了自己的ClassLoader，便可以做到如下几点: 1. 在执行非置信代码之前，自动验证数字签名。2. 动态地创建符合用户特定需要的定制化构建类。 3.从特定的场所取得java class，例如数据库中和网络中。
URLClassLoader：这是一个常见的用户自定义类加载器，可以从指定的URL加载类。在很多情况下，当需要从外部加载一些类或JAR文件时，使用URLClassLoader是比较方便的。URLClassLoader是Application ClassLoader的子类加载器。

JVM类加载机制

全盘负责，当一个类加载器负责加载某个Class时，该Class所依赖的和引用的其他Class也将由该类加载器负责载入，除非显示使用另外一个类加载器来载入
父类委托，先让父类加载器试图加载该类，只有在父类加载器无法加载该类时才尝试从自己的类路径中加载该类
缓存机制 ，缓存机制将会保证所有加载过的Class都会被缓存，当程序中需要使用某个Class时，类加载器先从缓存区寻找该Class，只有缓存区不存在，系统才会读取该类对应的二进制数据，并将其转换成Class对象，存入缓存区。这就是为什么修改了Class后，必须重启JVM，程序的修改才会生效
双亲委派机制，如果一个类加载器收到了类加载的请求，它首先不会自己去尝试加载这个类，而是把请求委托给父加载器去
完成，依次向上，因此，所有的类加载请求最终都应该被传递到顶层的启动类加载器中，只有当父加载器在它的搜索范围中没有找到所需的类时，即无法完成该加载，子加载器才会尝试自己去加载该类。
在Java中如何使用代码的方式去主动加载一个类呢?
方式1：使用Class.forName方法，使用当前类的类加载器去加载指定的类
方式2：获取到类加载器，通过类加载器的loadClass方法指定某个类加载器加载

双亲委派机制

由于Java虚拟机中有多个类加载器，双亲委派机制的核心是解决一个类到底由谁加载的问题。
双亲委派机制指的是：当一个类加载器接收到加载类的任务时，会自底向上查找是否（被这个类加载器）加载过，再由顶向下（如果位于这个类加载器的加载目录中）进行加载。
双亲委派机制的好处有两点: 第一是避免恶意代码替换JDK中的核心类库，确保的完整性和安全性；二是避免一个类重复地被加载

打破双亲委派机制：

自定义类加载器
通常情况下，我们都是直接使用系统类加载器。但有时，我们也需要自定义类加载器。比如应用通过网络传输 Java 类的字节码，为保证安全性经过了加密处理，这时系统类加载器就无法对其进行加载；Tomcat通过自定义类加载器实现应用之间类隔离；
自定义类加载器一般都是继承自 ClassLoader 类，重写 findClass方法。

public class MyClassLoader extends ClassLoader {
    ...
    protected Class<?> findClass(String name) throws ClassNotFoundException {
        byte[] classData = loadClassData(name);
        if (classData == null) {  throw new ClassNotFoundException();
        } else {  return defineClass(name, classData, 0, classData.length);  // 连接阶段
        }
    }
    private byte[] loadClassData(String className) {
        String fileName = root + File.separatorChar
                + className.replace('.', File.separatorChar) + ".class";
        try {
            InputStream ins = new FileInputStream(fileName);
            ByteArrayOutputStream baos = new ByteArrayOutputStream();
            int bufferSize = 1024;
            byte[] buffer = new byte[bufferSize];
            int length = 0;
            while ((length = ins.read(buffer)) != -1) {
                baos.write(buffer, 0, length);
            }
            return baos.toByteArray();
        } catch (IOException e) {
            e.printStackTrace();
        }
        return null;
    }
    ...
    public static void main(String[] args)  {
        MyClassLoader classLoader = new MyClassLoader();
        classLoader.setRoot("D:\\temp");
        Class<?> testClass = null;
        try {
            testClass = classLoader.loadClass("com.pdai.jvm.classloader.Test2");
            Object object = testClass.newInstance();
            System.out.println(object.getClass().getClassLoader());
        } catch () {...        }
    }
}

线程上下文类加载器 ？？？实际上没打破。。？**?????????**
大量应用在 java底层，比如JDBC和JNDI等
Osgi框架的类加载器
历史上Osgi框架实现了一套新的类加载器机制，允许同级之间委托进行类的加载；还使用类加载器实现热部署功能。

JDK8 后的类加载器

由于JDK9引入了module的概念，类加载器在设计上发生了很多变化。

启动类加载器使用Java编写，位于jdk.internal.loader.ClassLoaders类中Java中的BootClassLoader继承自BuiltinClassLoader实现从模块中找到要加载的字节码资源文件.启动类加载器依然无法通过java代码获取到，返回的仍然是null，保持了统一。
扩展类加载器被替换成了平台类加载器(Platform Class Loader)
平台类加载器遵循模块化方式加载字节码文件，所以继承关系从URLClassLoader变成了BuiltinClassLoader，BuiltinClassLoader实现了从模块中加载字节码文件。平台类加载器的存在更多的是为了与老版本的设计方案兼容，自身没有特殊的逻辑

JVM 内存结构

Java 虚拟机在运行Java程序过程中管理的内存区域，称之为运行时数据区。！！注意不要和Java内存模型混淆了，，

Java 虚拟机定义了若干种程序运行期间会使用到的运行时数据区，其中有一些会随着虚拟机启动而创建，随着虚拟机退出而销毁。另外一些则是与线程一一对应的，这些与线程一一对应的数据区域会随着线程开始和结束而创建和销毁。【 类的生命周期的使用，卸载阶段？】
线程私有：程序计数器、虚拟机栈、本地方法区
线程共享：堆、方法区，堆外内存（Java7的永久代或JDK8的元空间、代码缓存）

程序计数器

程序计数器(Program Counter Register)也叫PC寄存器，每个线程会通过程序计数器记录当前要执行的的字节码指令的内存地址。
它是一块很小的固定大小的内存空间，不会发生内存溢出 "OutOfMemoryError"。

在代码执行过程中，程序计数器会记录下一行字节码指令的地址。执行完当前指令之后，虚拟机的执行引擎根据程序计数器执行下一行指令。程序计数器可以控制程序指令的进行，实现分支、跳转、异常等逻辑。
在多线程执行情况下，CPU会不停的做任务切换，这导致经常中断或恢复。JVM 需要通过程序计数器记录 CPU 切换前解释执行到那一句指令并继续解释运行。每个线程都有它自己的程序计数器，独立计算，不会互相影响。

Java 虚拟机栈

早期也叫 Java 栈。每个线程在创建的时候都会创建一个虚拟机栈，其内部保存一个个的栈帧(Stack Frame），对应着一次次 Java 方法调用，是线程私有的，生命周期和线程一致。
作用：主管 Java 程序的运行，它保存方法的局部变量、部分结果，并参与方法的调用和返回。
JVM栈采用栈的数据结构来管理方法调用中的基本数据，先进后出，每一个方法的调用使用一个栈帧(Stack Frame)来保存。
IDEA 在 debug 时候，可以在 debug 窗口看到 Frames 中各种方法的压栈和出栈情况
栈帧的组成
- 局部变量表：在运行过程中存放所以的局部变量，包括实例方法的this对象，方法的参数，方法体中声明的局部变量
  - 编译成字节码文件时就可以确定局部变量表的内容，包含局部变量的编号、生效范围等；
    局部变量表数据在 字节码文件 - 方法 - Code - LocalVariableTable 查看。
  - 实际在栈帧中，局部变量表是一个数组，数组中每一个位置为槽(slot)，long和double类型占两个槽，其他类型占一个。
  - 实例方法中的序号为0的位置存放的是this，指的是当前调用方法的对象，运行时会在内存中存放实例对象的地址。
  - 方法参数也会保存在局部变量表中，其顺序与方法中参数定义的顺序一致局部变量表
- 操作数栈：JVM在执行指令的过程中用来存放临时数据的一块区域。主要用于保存计算过程的中间结果，同时作为计算过程中变量临时的存储空间
  - 它是一种栈式的数据结构，如果一条指令将一个值压入操作数栈，则后面的指令可以弹出并使用该值。
  - 在编译期就可以确定操作数栈的最大深度，从而在执行时正确的分配内存大小
- 帧数据
  - 动态链接：当前类的字节码指令引用了其他类的属性或者方法时，需要将符号引用(编号)转换成对应的运行时常量池中的内存地址。动态链接就保存了编号到运行时常量池的内存地址的映射关系。
  - 方法出口：方法出口指的是方法在正确或者异常结束时，当前栈帧会被弹出，同时程序计数器应该指向上一个栈帧中的下一条指令的地址。所以在当前栈帧中，需要存储此方法出口的地址。
  - 异常表的引用：异常表存放代码中异常的处理信息，包含了try代码块和catch代码块执行后跳转到的字节码指令位置
栈内存溢出：一个线程的Java 虚拟机栈中，如果栈帧过多，占用内存超过栈内存可分配的最大大小就会出现内存溢出，出现StackOverflowError错误
- 如果我们不指定栈的大小，JVM 将创建一个具有默认大小的栈。大小取决于操作系统和计算机的体系结构，windows(64位)下的JDK8测试最小值为180k，最大值为1024m
- 要修改Java虚拟机栈的大小，可以使用虚拟机参数 -Xss。一般情况下，工作中即便使用了递归进行操作，栈的深度最多也只能到几百,不会出现栈的溢出。所以此参数可以手动指定为 -Xss256k 节省内存。

本地方法栈

Java虚拟机栈存储了Java方法调用时的栈帧，而本地方法栈存储的是（c++编写的）native本地方法（如文件IO操作）的栈帧.
在Hotspot虚拟机中，Java虚拟机栈和本地方法栈实现上使用了同一个栈空间。本地方法栈会在栈内存上生成一个栈帧，临时保存方法的参数，同时方便出现异常时也把本地方法的栈信息打印出来

`栈是运行时的单位，而堆是存储的单位`

栈解决程序的运行问题，即程序如何执行，或者说如何处理数据。堆解决的是数据存储的问题，即数据怎么放、放在哪。

堆

一般Java程序中堆内存是空间最大的一块内存区域。创建出来的对象都存在于堆上，并且在栈上保存一个对象的引用（在堆上的地址）。
达到上限之后，就会抛出 OutofMemory错误。
栈上的局部变量表中，可以存放堆上对象的引用。静态变量也可以存放堆对象的引用，通过静态变量就可以实现对象在线程之间共享。

堆内存中有三个值，used 指的是当前已使用的堆内存，total 是JVM已分配的可用堆内存，max 是JVM可以分配的最大堆内存。total 不足时，JVM会继续分配内存给堆，total 值增大但最多只能与 max 相等。
max 默认是系统内存的 1/4，total 默认是系统内存的 1/64。实际使用中一般都需要设置这两个值。
Java服务端程序开发时，建议将 -Xmx（max最大值）和 -Xms（初始的total）设置为相同的值，避免再次申请内存。

方法区

方法区是存放基础信息的位置，线程共享，主要包括三部分；
- 类的元信息：类的基本信息 (元信息)，一般称之为InstanceKlass对象。在类的加载阶段完成.
- 运行时常量池：放的是字节码中的常量池内容。字节码文件中通过编号查表的方式找到常量，这种常量池称为静态常量池。当常量池加载到内存中之后，可以通过内存地址快速的定位到常量池中的内容，这种常量池称为运行时常量池
- 字符串常量池：字符串常量池存储在代码中定义的常量字符串内容。比如String s2 = “abc” 的 “abc”即 s2这个字符串常量就会被放入字符串常量池（而String s1 = new String(“abc”) 中的 s1这个对象会被放入堆内存）
方法区是《Java虚拟机规范》中设计的虚拟概念，每款Java虚拟机在实现上都各不相同。Hotspot设计如下
- JDK7及之前的版本将方法区存放在堆区域中的永久代空间，堆的大小由虚拟机参数来控制。
- JDK8及之后的版本将方法区存放在元空间中，元空间位于OS维护的直接内存中，默认在不超过OS承受的上限可以一直分配
- ！！ JDK6中字符串常量池在方法区（永久代）中，永久代在堆中；JDK7中从字符串常量池永久代中移出，仍在堆中；而JDK8后方法区（永久代->元空间）从堆中移出，字符串常量池仍在堆中

直接内存

直接内存(Direct Memory)并不在《Java虚拟机规范》中存在，所以并不属于Java运行时的内存区域.

在JDK1.4中引入了NIO机制，使用了直接内存，主要为了解决以下两个问题:
1、Java堆中的对象如果不再使用要回收，回收时会影响对象的创建和使用。
2、I0操作比如读文件，需要先把文件读入直接内存(缓冲区)再把数据复制到Java堆中现在直接放入直接内存即可，同时Java堆上维护直接内存的引用，减少了数据复制的开销。写文件也是类似的思路.
要创建直接内存上的数据，可以使用ByteBuffer。语法: ByteBuffer directBuffer = ByteBuffer.allocateDirect(size);
注意事项: arthas的memory命令可以查看直接内存大小，属性名direct。

Java 内存模型

？？
？

JVM GC 垃圾回收

在C/C++这类没有自动垃圾回收机制的语言中，一个对象如果不再使用，需要手动释放，否则就会出现内存泄漏。内存泄漏指的是不再使用的对象在系统中未被回收，内存泄漏的积累可能会导致内存溢出。
Java中为了简化对象的释放，引入了自动的垃圾回收 (Garbage Collection 简称 GC) 机制。【 类的生命周期的卸载阶段 ？？】
线程不共享的部分，都是伴随着线程的创建而创建，线程的销毁而销毁。而方法的栈帧在执行完方法之后就会自动弹出栈并释放掉对应的内存。所以只用考虑线程不共享部分。JVM GC主要负责对堆上的内存进行回收。

方法区的回收

方法区中能回收的内容主要就是不再使用的类.判定一个类可以被卸载。需要同时满足下面三个条件
1、此类所有实例对象都已经被回收，在堆中不存在任何该类的实例对象以及子类对象。
2、加载该类的类加载器已经被回收
3、该类对应的java.lang.Class 对象没有在任何地方被引用
开发中此类场景一般很少出现，主要在如 OSGi、JSP 的热部署等应用场景中。

堆的回收

如何判断堆上的对象可以回收? Java中的对象是否能被回收，是根据对象是否被引用来决定的。引用说明该对象还在使用，不允许被回收。

常见的有两种判断方法:引用计数法和可达性分析法。

引用计数法：会为每个对象维护一个引用计数器，当对象被引用时加1，取消引用时减1.
- 优点是实现简单，C++中的智能指针就采用了引用计数法
- 缺点主要有两点: 1.每次引用和取消引用都需要维护计数器，对系统性能会有一定的影响 2.存在循环引用问题，所谓循环引用就是当A引用B，B同时引用A时会出现对象无法回收的问题
可达性分析算法：Java使用的是可达性分析算法来判断对象是否可以被回收。可达性分析将对象分为两类:垃圾回收的根对象GRoot)和普通对象，对象与对象之间存在引用关系。如果其（反向？引用）到某个GC Root对象是可达的，对象就不可被回收。
- 四大类 GCRoot 对象
  - 线程Thread对象（放在堆中，指向对应的栈）
  - 系统类加载器加载的java.lang.Class对象，引用类中的静态变量 ???、，，？？
  - 监视器对象，用来保存同步锁 synchronized关键字持有的对象
  - 本地方法调用时使用的全局对象

五种引用

强引用：可达性算法中描述的一般指的是强引用，即是GCRoot对象对普通对象有引用关系，只要关系存在普通对象就不会被回收。

软引用：相对于强引用是一种比较弱的引用关系

如果一个对象只有软引用关联到它，当程序内存不足时，就会将软引用中的数据进行回收。
软引用常用于缓存中（提高效率，不影响可用性）

在JDK 1.2版之后提供了sftReference类来实现软引用。软引用的执行过程如下：
1.将对象使用软引用包装起来，new SoftReference<对象类型>(对象)
2.内存不足时，虚拟机尝试进行垃圾回收。
3.如果垃圾回收仍不能解决内存不足的问题，回收软引用中的对象
4.如果依然内存不足，抛出OutofMemory异常

byte[] bytes = new byte[1024 * 1024 * 100];    // 建立数组（强引用对象？？                
SoftReference<byte[]> softReference = new SoftReference<byte[]>(bytes);  // 建立软引用
bytes = null;                                  // 释放强引用
System.out.println(softReference.get());       // ：[B@2503dbd3
byte[] bytes2 = new byte[1024 * 1024 * 100];   // 内存不足，释放软引用对象
System.out.printIn(softReference.get());       // ：null
byte[] bytes2 = new byte[1024 * 1024 * 100];   // ：直接抛OutofMemory异常

？？？软引用队列：软引用中的对象如果在内存不足时回收，SoftReference对象本身也需要被回收。如何知道哪些SoftReference对象需要回收呢? SoftReference提供了一套队列机制:1、软引用创建时，通过构造器传入引用队列2、在软引用中包含的对象被回收时，该软引用对象会被放入引用队列3通过代码遍历引用队列，将SoftReference的强引用删除

弱引用：弱引用的整体机制和软引用基本一致，区别在于弱引用包含的对象在垃圾回收时不管内存够不够都会直接被回收
在JDK1.2版之后提供了WeakReference类来实现弱引用，弱引用主要在ThreadLocal中使用。
弱引用对象本身也可以使用引用队列进行回收。
虚引用：虚引用也叫幽灵引用/幻影引用，不能通过虚引用对象获取到包含的对象。虚引用唯一的用途是当对象被垃圾回收器回收时可以接收到对应的通知。Java中使用PhantomReference实现了虚引用，直接内存中为了及时知道直接内存对象不再使用，从而回收内存，使用了虚引用来实现。
终结器引用：指的是在对象需要被回收时，对象将会被放置在Finalizer类中的引用队列中，并在稍后由一条由FinalizerThread线程从队列中获取对象，然后执行对象的finalize方法。在这个过程中可以在finalize方法中再将自身对象使用强引用关联上，但是不建议这样做，如果耗时过长会影响其他对象的回收。

垃圾回收算法

垃圾回收要做的有两件事：1、找到内存中存活的对象； 2、释放不再存活对象的内存，使得程序能再次利用这部分空间
三种评价标准：堆使用效率、吞吐量，以及最大停时间不可兼得。
一般来说，堆内存越大，最大暂停时间就越长。想要减少最大暂停时间，就会降低吞吐量。不同的垃圾回收算法，适用不同的场景。
标记清除算法
- 核心思想：1.标记阶段，将所有存活的对象进行标记。Java中使用可达性分析算法，从GC Root开始通过引用链遍历出所有存活对象。 2.清除阶段，从内存中删除没有被标记也就是非存活对象
- 优点：实现简单，只需要在第一阶段给每个对象维护标志位，第二阶段删除对象即可。
- 缺点：1.碎片化问题由于内存是连续的，所以在对象被删除之后，内存中会出现很多细小的可用内存单元。如果我们需要的是一个比较大的空间，很有可能这些内存单元的大小过小无法进行分配 2.分配速度慢。由于内存碎片的存在，需要维护一个空闲链表，极有可能发生每次需要遍历到链表的最后才能获得合适的内存空间。
复制算法
- 核心思想: 1.准备两块空间From空间和To空间，每次在对象分配阶段，只能使用其中一块空间 (From空间) 2.在垃圾回收GC阶段，将From中存活对象复制到To空间。 3.将两块空间的From和To名字互换
- 优点：吞吐量高、不会发生碎片化
- 缺点：内存使用效率低，每次只能让一半的内存空间来为创建对象使用
标记整理算法：也叫标记压缩算法，是对标记清理算法中容易产生内存碎片问题的一种解决方案.
- 核心思想：1.标记阶段，将所有存活的对象进行标记。Java中使用可达性分析算法，从GC Root开始通过引用链遍历出所有存活对象 2.整理阶段，将存活对象移动到堆的一端。清理掉存活对象的内存空间
- 优点：内存使用效率高，不会发生碎片化
- 缺点：整理阶段的效率不高

分代垃圾回收算法

分代垃圾回收算法(GenerationalGC)：将上述描述的垃圾回收算法组合进行使用，
- 它根据对象存活周期将内存划分为几块，不同块采用适当的收集算法
- 一般将堆分为新生代和老年代。新生代使用: 复制算法；老年代使用: 标记清除或者标记整理算法
- 将新生代划分为一块较大的 Eden 空间和两块较小的 Survivor 空间，每次使用 Eden 空间和其中一块 Survivor。在回收时，将 Eden 和 Survivor 中还存活着的对象一次性复制到另一块 Survivor 空间上，最后清理 Eden 和使用过的那一块 Survivor。
- HotSpot 虚拟机的 Eden 和 Survivor 的大小比例默认为 8:1，保证了内存的利用率达到 90%。如果每次回收有多于 10% 的对象存活，那么一块 Survivor 空间不够用，此时需要依赖于老年代进行分配担保，即借用老年代的空间存储放不下的对象。
- 系统中的大部分对象，都是创建出来之后很快就不再使用可以被回收，比如用户获取订单数据，订单数据返回给用户之后就可以释放了。老年代中会存放长期存活的对象，比如Spring的大部分bean对象，在程序启动之后就不会被回收了。
  在虚拟机的默认设置中，新生代大小要远小于老年代的大小。
- 分代GC算法将堆分成年轻代和老年代主要原因有：
  1、可以通过调整年轻代和老年代的比例来适应不同型的应用程序，提高内存的利用率和性能。 2、新生代和老年代使用不同的垃圾回收算法，新生一般选择复制算法，老年代可以选择标记-清除和标记-整理算法，由程序员来选择灵活度较高。 3、分代的设计中允许只回收新生代 (minor gc)，如果能满足对象分配的要求就不需要对整个堆进行回收(fullgc),STW时间就会减少
内存分配策略
1. 分代回收时，创建出来的对象，首先会被放入Eden伊甸园区。随着对象在Eden区越来越多，如果Eden区满，新创建的对象已经无法放入，就会触发年轻代的GC，称为Minor GC或者Young GC
  大对象直接进入老年代：大对象是指需要连续内存空间的对象，最典型的大对象是那种很长的字符串以及数组。经常出现大对象会提前触发垃圾收集以获取足够的连续空间分配给大对象。
  -XX:PretenureSizeThreshold，大于此值的对象直接在老年代分配，避免 Eden 和 Survivor 区之间的大量内存复制。
2. Minor GC 会把需要 eden中和 From需要回收的对象回收，把没有回收的对象放入To区。接下来，S0会变成To区，S1变成From区。当eden区满时再往里放入对象，依然会发生Minor GC此时会回收eden区和S1(from)中的对象，并把eden和from区中剩余的对象放入SO。！！如果to区满了，会将没有回收的对象放入老年代。
  注意:每次Minor GC中都会为对象记录他的年龄，初始值为0，每次GC完加1。
3. 长期存活的对象进入老年代：为对象定义年龄计数器，对象在 Eden 出生并经过 Minor GC 依然存活，将移动到 Survivor 中，年龄就增加 1 岁，增加到一定年龄则移动到老年代中。-XX:MaxTenuringThreshold 用来定义年龄阈值。
  动态对象年龄判定：虚拟机并不是永远地要求对象的年龄必须达到 MaxTenuringThreshold 才能晋升老年代，，，
4. 当老年代中空间不足，无法放入新的对象时，先尝试minor gc（因为存在直接从 eden区放如老年代的情况）。如果还是不足，就会触发Full GC，Full GC会对整个堆进行垃圾回收。如果Full GC依然无法回收掉老年代的对象，那么当对象继续放入老年代时，就会抛出OutofMemory异常。
5. 空间分配担保：在发生 Minor GC 之前，虚拟机先检查老年代最大可用的连续空间是否大于新生代所有对象总空间，如果条件成立的话，那么 Minor GC 可以确认是安全的。
  如果不成立的话虚拟机会查看 HandlePromotionFailure 设置值是否允许担保失败，如果允许那么就会继续检查老年代最大可用的连续空间是否大于历次晋升到老年代对象的平均大小，如果大于，将尝试着进行一次 Minor GC；如果小于，或者 HandlePromotionFailure 设置不允许冒险，那么就要进行一次 Full GC。
Full GC 的触发条件
对于 Minor GC，其触发条件非常简单：当 Eden 空间满时就将触发一次。而 Full GC 则相对复杂，有以下条件：
1.调用 System.gc() 2. 老年代空间不足 3. 空间分配担保失败 4. JDK 1.7及以前的永久代空间不足在 5. Concurrent Mode Failure
内存回收策略
Minor GC、Major GC、Full GC
JVM 在进行 GC 时，并非每次都对堆内存(新生代、老年代，方法区)区域一起回收的，大部分时候回收的都是指新生代。针对 HotSpot VM 的实现，它里面的 GC 按照回收区域又分为两大类: 部分收集 (Partial GC)，整收集(Full GC)。
- 部分收集: 不是完整收集整个 Java 堆的垃圾收集。其中又分为:
  1. 新生代收集 (Minor GC/Young GC) : 只是新生代的垃圾收集。
  2. 老年代收集 (Major GC/Old GC) : 只是老年代的垃圾收集
    目前，只有 CMS GC 会有单独收集老年代的行为。很多时候 Major GC 会和 Full GC 混合使用，需要具体分辨是老年代回收还是整堆回收
  3. 混合收集 (Mixed GC) : 收集整个新生代以及部分老年代的垃圾收集；目前只有 G1 GC 会有这种行为
- 整堆收集 (Full GC) : 收集整个 Java 堆和方法区的垃圾

垃圾回收器

垃圾回收器是垃圾回收算法的具体实现
由于垃圾回收器分为年轻代和老年代，除了G1之外其他垃圾回收器必须成对组合进行使用。

Serial + Serial Old 收集器

	Serial	Serial Old
	单线程串行回收年轻代的垃圾回收器	Serial垃圾回收器老年代版本，采用单线程串行回收
	年轻代，复制算法	老年代，标记-整理算法
优点	单CPU处理器下吞吐量非常出色
缺点	多CPU下吞吐量不如其他垃圾回收器，堆如果偏大会让用户线程处于长时间的等待
适用场景	Java编写的客户端程序或者硬件配置有限的场景	与Serial垃圾回收器搭配使用或者在CMS特殊情况下使用

ParNew + CMS 收集器

	ParNew	CMS
	本质上是对Serial在多CPU下的优化，使用多线程进行垃圾回收	关注的是系统的暂停时间。允许用户线程和垃圾回收线程在某些步骤中同时执行，减少了用户线程的等待时间。
参数	-XX:+UseParNewGC 新生代使用ParNew，回收器老年代使用串行回收器	XX:+UseConcMarkSweepGC
	年轻代，复制算法	老年代，标记-清除算法
优点	多CPU处理器下停顿时间较短	系统由于垃圾回收出现的停顿时间较短，用户体验好
缺点	吞吐量和停顿时间不如G1，所以在JDK9之后不建议使用	1、内存碎片问题 2、退化问题 3、浮动垃圾问题
适用场景	Java编写的客户端程序或者硬件配置有限的场景	大型的互联网系统中用户请求数据量大、频率高的场景，比如订单接口、商品接口等

ParNew + CMS 收集器

	Parallel Scavenge	Parallel Old
	JDK8默认的年轻代垃圾回收器多线程并行回收，关注的是系统的吞吐量。具备自动调整堆内存大小的特点	是为Parallel Scavenge收集器设计的老年代版本，利用多线程并发收集。
参数		-XX:+UseParallelGC 或-XX:+UseParallelOldGC，可以使用Parallel Scavenge + Parallel Old这种组合
	年轻代，复制算法	老年代，标记-整理算法
优点	吞吐量高，而目手动可控为了提高吞吐量，虚拟机会动态调整堆的参数	并发收集，在多核CPU下效率较高
缺点	不能保证单次的停顿时间	暂停时间会比较长
适用场景	后台任务，不需要与用户交互，并且容易产生大量的对象。比如:大数据的处理，大文件导出	与Parallel Scavenge配套使用

垃圾回收器的组合关系虽然很多，但是针对几个特定的版本，比较好的组合选择如下:
JDK8及之前：ParNew + CMS (关注暂停时间)、Parallel Scavenge + Parallel Old (关注吞吐量)、不建议 G1(较大堆并且关注暂停时间)
JDK9之后：G1 (默认)

G1收集器

它是一款面向服务端应用的垃圾收集器，在多 CPU 和大内存的场景下有很好的性能。使命是未来可以替换掉 CMS 收集器。
G1 将 Parallel Scavenge与 CMS的优点融合：1.支持巨大的堆空间回收，并有较高的吞吐量。2.支持多CPU并行垃圾回收 3.允许用户设置最大暂停时间。
G1 把堆划分成多个大小相等的独立区域(Region)，新生代和老年代不再物理隔离，可以直接对新生代和老年代一起回收。
G1垃圾回收有两种方式：1、年轻代回收 (Young GC) 2、混合回收(Mixed GC)
- 年轻代回收：回收Eden区和Survivor区中不用的对象。会导致STW，G1中可以通过参数设置每次垃圾回收时的最大暂停时间毫秒数，G1垃圾回收器会尽可能地XX:MaxGCPauseMillis=n (默认200) 保证暂停时间。
- 混合回收分为：初始标记 (initial mark) 、并发标记 (concurrent mark)、最终标记(remark或者FinalizeMarking)、并发清理 (cleanup) ；G1对老年代的清理会选择存活度最低的区域来进行回收，这样可以保证回收效率最高，这也是G1(Garbagefirst)名称的由来。
- 注意:如果清理过程中发现没有足够的空Region存放转移的对象，会出现Full GC。单线程执行标记-整理算法此时会导致用户线程的暂停。所以尽量保证应该用的堆内存有一定多余的空间。
G1 执行流程
1、新创建的对象会存放在Eden区。当G1判新年轻代区不足(max默认60%)，无法分配对象时需要回收时会执行Young GC
2、标记出Eden和Survivor区域中的存活对象
3、根据配置的最大暂停时间选择某些区域将存活对象复制到一个新的Survivor区中(年龄+1)，清空这些区域
4、后续Young GC时与之前相同，只不过Survivor区中存活对象会被搬运到另一个Survivor区
5、当某个存活对象的年龄到达值 (默认15)，将被放入老年代
6、部分对象如果大小超过Region的一半，会直接放入老年代，这类老年代被称为Humongous区。比如堆内存是4G，每个Region是2M，只要一个大对象超过了1M就被放入Humonous区，如果对象过大会横跨多个Region。
7、多次回收之后，会出现很多Old老年代区，此时总堆占有率达到闻值时(-XX:InitiatingHeap0ccupancyPercent默认45%)
会触发混合回收MixedGC。回收所有年轻代和部分老年代的对象以及大对象区。采用复制算法来完成？？？不会产生内存碎片

JVM 排错调优

？？

JVM 知识体系

2021-09-02

Java 数据结构

数组

数组是一种连续存储线性结构，数组尺寸不能改变。元素类型相同，大小相等，通过使用整型索引值来访问他们的元素。数组是多维的。数组能够容纳基本数据类型（int、char等）或者对象引用（如类对象）。
数组的优点：存取速度快
数组的缺点：事先必须知道数组的长度、插入删除元素很慢、空间通常有限制、需要大块连续内存块、插入删除元素的效率很低
Java没有指针，同时也不对程序员暴露其元素的地址，寻址操作完全交给虚拟机。所以看不到每个元素的地址情况

int[] numbers;                               // 声明一个 int 数组
numbers = new int[5];                        // 初始化一个长度为 5 的 int 数组
int[] values = {1, 2, 3, 4, 5};              // 声明并初始化一个 int 数组
... return new int[]{i, j};                  // 在方法中返回数组[i, j]
int length = arr.length;                     // 获取数组的长度
int value = arr[1];                          // 获取索引为 1 的元素
int[][] twoDimArray = new int[3][4];         // 创建一个 3x4 的二维数组
int[][] twodimArray = {{1,6},{7,3},{1,5}};   // 声明并初始化一个 二维 int 数组
int[][][] threeDimArray = new int[3][4][2];  // 创建一个 3x4x2 的三维数组
System.out.println(twoDimArray[0]);          // [I@7852e922：16进制数值，不是真正的地址，是处理后的

int[] numbers; 只是声明了一个名为 numbers 的整数数组的引用，它并没有创建数组对象，并没有分配内存或存储数据。
int[] numbers = new int[5]; 在这里，new int[5] 表示创建一个能够存储 5 个整数的整型数组，并将该数组的引用赋给 numbers 变量。这是一个基本的数组类型，而不是 Arrays、ArrayList 或 Vector 对象。
数组是基本的数据结构，而 Arrays 和 ArrayList 是 Java 中的类，提供了用于操作和管理数组的方法。

Arrays

Arrays 类是 Java API 中的一个工具类，它提供了一系列静态方法来操作数组，比如排序、搜索、比较等。

int[] arr = new int[5];
Arrays.fill(arr, 10);                           //  fill()：将数组的所有元素设置为指定值。
String[] array = {"apple", "banana", "orange"};
List<String> list = Arrays.asList(array);       //  asList()：将数组转换为 `List`。
int[] numbers = {5, 2, 9, 1, 5};
Arrays.sort(numbers);                           //  sort()：对数组进行排序。
int index = Arrays.binarySearch(numbers, 3);    //  binarySearch()：在排序数组中执行二分查找。
String str = Arrays.toString(numbers);          //  toString()：将数组转换为字符串表示形式。
boolean isEqual = Arrays.equals(arr, numbers);  //  equals()：比较两个数组是否相等。
int[] copy1 = Arrays.copyOf(arr, sou.length);   //  copyOf：复制数组或复制数组的指定范围。
int[] copy2 = Arrays.copyOfRange(arr, 2, 4);    //  copyOfRange()：复制数组或复制数组的指定范围。

Vector

Vector 是一个同步的动态数组类，类似于 ArrayList，可以自动增长和缩小以容纳对象。
ArrayList 和 Vector 都是动态数组实现的集合，而 Arrays 类主要用于数组的各种操作。
Vector 是线程安全的（是同步的），而 Arrays 不是（没有提供同步）。Vector 在对集合进行操作时会进行同步，适用于多线程环境。单线程环境下，推荐使用 ArrayList 而不是 Vector，因为 ArrayList 不是同步的，性能更高。

Vector<String> vector = new Vector<>();            // 创建 Vector
vector.add("Element 1");                           // 添加元素
int size = vector.size();                          // 获取 Vector 的大小
boolean isEmpty = vector.isEmpty();                // 检查 Vector 是否为空
String element = vector.get(0);                    // 访问 Vector 中的元素：获取索引为0的元素
int index = vector.indexOf("Element 2");           // 查找元素在 Vector 中的位置
vector.remove(1);                                  // 删除 Vector 中的元素：删除索引为1的元素
for (String element : vector) { ...}               // 遍历 Vector 中的元素

ArrayList

ArrayList是基于动态数组实现的，可以自动扩容。（动态数组是一种数据结构，而非类，是一种具有自动扩容能力的数组）
它支持快速随机访问元素，但在插入和删除元素时可能会比较耗时。适用于需要随机访问元素、按索引查找和遍历集合的场景。
1、add(E e)：在尾部添加元素。
2、get(int index)：获取指定位置的元素。
3、set(int index, E element)：用于替换指定索引处的元素。
4、remove(int index)：移除指定位置的元素。
5、size()：返回集合大小。

1
2
3

List<String> cur = new ArrayList<>();                        // 一维动态数组
List<List<Integer>> ans = new ArrayList<List<Integer>>();    // 二维动态数组
ans.get(i).set(j, ans.get(i).get(j) + ans.get(i-1).get(j));  // 二维数组读写

LinkedList

LinkedList是基于双向链表实现的，每个节点都存储了对前一个和后一个元素的引用。它在插入和删除元素时效率较高，但在随机访问元素时效率较低。LinkedList适用于需要频繁的插入、删除操作的场景。
1、add(E e)：在尾部添加元素。
2、addFirst(E e)：在头部添加元素。
3、get(int index)：获取指定位置的元素。
4、remove(int index)：移除指定位置的元素。
5、size()：返回集合大小。

链表

链表由一个节点序列组成，每个节点包含数据和指向下一个节点的引用。n个节点离散分配，每个节点只有一个前驱节点和一个后续节点，首节点没有前驱节点，尾节点没有后续节点。当你创建一个链表时，你持有的引用实际上指向链表中第一个节点的地址，也就是头节点。头节点存储了链表的起始地址，通过这个地址可以访问整个链表。
链表优点：空间没有限制、插入删除元素很快。链表缺点：存取速度很慢

单链表

单链表的每个节点包含两个部分：数据和指向下一个节点的引用。第一个节点称为头节点，最后一个节点的下一个节点为空null

public class Node {   // Java中单链表的节点（Node）通常会被定义为一个内部类。
    public int data;  // 数据域
    public Node next; // 指针域，指向下一个节点
    public Node() {    }
    public Node(int data) {        this.data = data;    }
    public Node(int data, Node next) {        this.data = data;        this.next = next;    }
}

public class SinglyLinkedList {
    private Node head;
    // 添加新节点
    public void addNode(int data) {
        Node newNode = new Node(data);
        if (head == null) {
            head = newNode;
        } else {
            Node current = head;
            while (current.next != null) {
                current = current.next;
            }
            current.next = newNode;
        }
    }
    // 其他操作（删除节点、查找节点等）可以根据需要实现
}

双向链表 中的每个节点都有两个指针：一个指向前一个节点，一个指向后一个节点。双向链表允许在节点之间双向遍历。
将两种(双向/单向)链表的最后一个结点指向第一个结点从而实现 循环链表，能通过任何一个节点找到其他所有的节点。

哈希表

散列表（Hash table，也叫哈希表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。哈希表使用 O(N) 空间复杂度存储数据，并且以 O(1) 时间复杂度求解问题。

构造散列函数的方法有：
1. 直接定址法：取关键字或关键字的某个线性函数值为散列地址。即：h(key) = key 或 h(key) = a * key + b，其中 a，b 为常数
2. 数字分析法
3. 平方取值法：取关键字平方后的中间几位为散列地址。
4. 折叠法：将关键字分割成位数相同的几部分，然后取这几部分的叠加和作为散列地址。
5. 除留余数法：取关键字被某个不大于散列表表长 m 的数 p 除后所得的余数为散列地址，即： h(key) = key MOD p p ≤ m
6. 随机数法：选择一个随机函数，取关键字的随机函数值为它的散列地址，即： h(key) = random(key)

使用了散列表的集合有map和set；

HashSet 用于存储一个集合，可以查找元素是否在集合中。
但是，如果元素有穷，并且范围不大，那么可以用一个布尔数组来存储一个元素是否存在，就足够了。
HashMap 主要用于映射关系，从而把两个元素联系起来。HashMap 也可以用来对元素进行计数统计，此时键为元素，值为计数。和 HashSet 类似，如果元素有穷并且范围不大，可以用整型数组来进行统计。

HashMap 常用方法

put(key, value)：将指定的键值对添加到哈希表中；如果该键已存在于 HashMap 中，则其旧值会被新值替换。
get(key)：根据键获取对应的值。
containsKey(key)：检查哈希表中是否包含指定的键。containsValue(value)：检查哈希表中是否包含指定的值。
remove(key)：根据键移除键值对。
size()：返回哈希表中键值对的数量。
isEmpty()：检查哈希表是否为空。
keySet()：返回哈希表中所有键的集合。values()：返回哈希表中所有值的集合。entrySet()：返回键值对的集合。

import java.util.HashMap;
import java.util.Map;
Map<String, Integer> hashMap = new HashMap<>();  // 创建一个HashMap
hashMap.put("Three", 3);  hashMap.remove("Three");
if (!hashMap.containsKey("Three"))  hashMap.put("Three", 3); 
// 遍历kv：2种方法
for (Map.Entry<String, Integer> entry : hashMap.entrySet()) {  
    System.out.println("Key: " + entry.getKey() + ", Value: " + entry.getValue());
}
for(String s : hashMap.keySet()) System.out.println("Key: " + s + ", Value: " + hashMap.get(s));

HashSet 常用方法

add(E e): 向集合中添加元素。addAll(Collection<? extends E> c): 将另一个集合的所有元素添加到当前集合。
remove(Object o): 移除指定的元素。removeAll(Collection<?> c): 移除当前集合中包含在指定集合中的所有元素。
contains(Object o): 判断集合中是否包含指定元素。containsAll(Collection<?> c): 判断集合是否包含指定集合中的所有元素。
size(): 返回集合的大小（元素个数）。
isEmpty(): 判断集合是否为空。
clear(): 清空集合中的所有元素。
iterator(): 返回用于遍历集合的迭代器。

字符串

String 内部使用 char 数组存储数据。该数组被声明为 final，因此它不可被继承，初始化之后就不能再引用其它数组。并且 String 内部没有改变 value 数组的方法，因此可以保证 不可变。String 是一个类，而不是基本数据类型或容器。表示的是一个字符序列。
字符串是一个引用类型，因此在创建 String 对象时，实际上是在内存中分配了一块存储空间来存储字符串的值。(字符串常量池，堆，栈，

获取字符串信息：
length()：返回字符串的长度。
charAt(int index)：返回指定索引处的字符。
substring(int beginIndex)：返回从 beginIndex 开始到字符串末尾的子字符串。
substring(int beginIndex, int endIndex)：返回从 beginIndex 到 endIndex（不含）之间的子字符串
字符串拼接：直接使用 + 运算符，或 concat(String str)：将指定字符串 str 连接到原字符串的末尾。
String 不可变，+= 操作符或 concat()实际上创建了一个新的字符串对象，该对象包含字符串值修改后的内容，然后将其分配给了原 str变量，使 str 引用了新的字符串对象，而原始的空字符串对象仍然存在，没有被修改。
字符串查找和比较：
indexOf(String str)：返回指定子字符串 str 在主字符串中第一次出现的位置。lastIndexOf()：返回最后一次..
equals(Object another)：比较两个字符串是否相等。equalsIgnoreCase()：忽略大小写比较..。
字符串转换：
toLowerCase()：将字符串转换为小写，toUpperCase()：转大写。对于字符，有 Character.toLowerCase() 方法；
trim()：去除字符串首尾的空格。

切割字符串：

String text = "Hello world! This is a Java example.";
// split() 方法根据匹配给定的正则表达式来拆分字符串。(注意判断结果可能是空字符串)
// 注意：`.`、`$`、`|` 和 `*` 等转义字符，必须得加 \\。多个分隔符，可以用 | 作为连字符。
// 使用空格切割字符串: \\s+ 表示一个或多个空格
String[] words = text.split("\\s+");

字符串替换：
replace(char oldChar, char newChar)：将字符串中的 oldChar 替换为 newChar。
replaceAll(String regex, String replace)：使用新字符串replace替换所有与 regex匹配的字符串。
replaceFirst(String regex, String replacement)：替换第一个匹配的字符串。

字符串翻转：

1
2
3

String original = "Hello, World!";
StringBuffer reversed = new StringBuffer(original).reverse();
String reversedString = reversed.toString();

栈和队列

数组和链表都是线性存储结构的基础，栈和队列都是线性存储结构的应用

栈（Stack）

栈是一种后进先出（LIFO，Last-In-First-Out）的数据结构。在Java中，可以使用 java.util.Stack 类实现栈的功能，也可以使用 Deque 接口（比如 ArrayDeque 或 LinkedList）来模拟栈的行为。
Java 中，Stack 类实际上继承自 Vector 类。Vector 类实现了一个动态数组，而 Stack 在 Vector 的基础上提供了栈的常见操作。

import java.util.Stack;
Stack<Integer> stack = new Stack<>();
stack.push(10);                       // push(E item)：将元素压入栈顶。
stack.push(20); 
System.out.println(stack.pop());      // pop()：移除并返回栈顶元素。输出 30
System.out.println(stack.peek());     // peek()：返回但不移除栈顶元素。输出 20
System.out.println(stack.isEmpty());  // isEmpty()：检查队列是否为空。输出 false

队列（Queue）

队列是一种先进先出（FIFO，First-In-First-Out）的数据结构。在Java中，可以使用 java.util.Queue 接口和它的实现类来实现队列。

import java.util.LinkedList;
import java.util.Queue;
Queue<Integer> queue = new LinkedList<>();
queue.offer(10);                        // offer(E e)：将元素插入队列。
queue.offer(20);
int count = que.size();                 // 队列的大小
System.out.println(queue.poll());       // poll()：移除并返回队列头部的元素。输出 10
System.out.println(queue.peek());       // peek()：返回但不移除队列头部的元素。输出 20
System.out.println(queue.isEmpty());    // isEmpty()：检查队列是否为空。输出 false

双向队列 (Deque, “double ended queue”)，它可以从队列的两端添加和删除元素。Java的java.util包提供了ArrayDeque和LinkedList两种实现。

Deque<String> stack = new ArrayDeque<String>();  
if (!stack.isEmpty()) {
    stack.pollFirst();      // 前出
} else {
    stack.offerLast(name);  // 后入
}

优先级队列 (PriorityQueue), 是一个无界队列，它使用元素的自然顺序或者构造队列时提供的Comparator对元素进行排序。PriorityQueue不允许使用null元素。

// 创建一个基于自然顺序的优先级队列  
PriorityQueue<Integer> queue = new PriorityQueue<>();  
// 添加元素  
queue.add(3);  
queue.add(1);  
queue.add(4);  
int removed = queue.poll();  // 取出并删除队列中的最小元素 
System.out.println(queue);   // 输出队列：3, 4

// 创建一个基于自定义Comparator的优先级队列  
PriorityQueue<Integer> queue = new PriorityQueue<>(Comparator.comparingInt(Math::abs));  
// 添加元素  
queue.add(-3);  
queue.add(-1);  
queue.add(4);  
queue.add(-2);  
System.out.println(queue);  // 输出队列：1, 2, 3, 4，因为它们的绝对值从小到大排列

树

树：它是n(n>=0)个节点的有限集。n=0时为空树。n>0时，有限集的元素构成一个具有层次感的数据结构。
区别于线性表一对一的元素关系，树中的节点是一对多的关系。树具有以下特点:
1、n>0时，根节点是唯一的，不可能存在多个根节点。
2、每个节点有零个至多个子节点；除了根节点外，每个节点有且仅有一个父节点。根节点没有父节点。

基本概念：
- 子树: 除了根节点外，每个子节点都可以分为多个不相交的子树。
- 孩子与双亲: 若一个结点有子树，那么该结点称为子树根的”双亲”，子树的根是该结点的”孩子”。
- 兄弟: 具有相同双亲的节点互为兄弟。
- 节点的度: 一个节点拥有子树的数目。
- 叶子: 没有子树，也即是度为0的节点。
- 分支节点: 除了叶子节点之外的节点，也即是度不为0的节点。
- 内部节点: 除了根节点之外的分支节点。
- 层次: 根节点为第一层，其余节点的层次等于其双亲节点的层次加1.
- 树的高度: 也称为树的深度，树中节点的最大层次。
- 有序树: 树中节点各子树之间的次序是重要的，不可以随意交换位置。
- 无序树: 树种节点各子树之间的次序是不重要的。可以随意交换位置。
- 森林: 0或多棵互不相交的树的集合。
二叉树：最多有两棵子树的树被称为二叉树
- 满二叉树: 二叉树中所有非叶子结点的度都是2，且叶子结点都在同一层次上
- 完全二叉树: 如果一个二叉树与满二叉树前m个节点的结构相同，这样的二叉树被称为完全二叉树
- 插入
- 删除
- 遍历：前序遍历、中序遍历、后序遍历
- 搜索
动态查找树
- 二叉搜索树 BST
  - 指一棵空树或者具有下列性质的二叉树：若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；任意节点的左、右子树也分别为二叉查找树；没有键值相等的节点。
  - 二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低为 O(logn) 。二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、多重集、关联数组等。
- 二叉平衡树 AVL
  - 含有相同节点的二叉查找树可以有不同的形态，而二叉查找树的平均查找长度与树的深度有关，所以需要找出一个查找平均长度最小的一棵，那就是平衡二叉树
  - 具有以下性质：要么是棵空树，要么其根节点左右子树的深度之差的绝对值不超过1；其左右子树也都是平衡二叉树；二叉树节点的平衡因子定义为该节点的左子树的深度减去右子树的深度。则AVL的所有节点的平衡因子只可能是-1,0,1。
- 红黑树
  - 红黑树也是一种自平衡的二叉查找树，它在每个节点增加了一个存储位记录节点的颜色，可以是RED,也可以是BLACK;通过任意一条从根到叶子简单路径上颜色的约束，红黑树保证最长路径不超过最短路径的二倍，因而近似平衡。
  - 特征：1、每个结点要么是红的要么是黑的。(红或黑) 2、根结点是黑的。(根黑) 3、每个叶结点(叶结点即指树尾端NIL指针或NULL结点)都是黑的。(叶黑) 4、如果一个结点是红的，那么它的两个儿子都是黑的。(红子黑) 5、对于任意结点而言，其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。(路径下黑相同)
  - 红黑树与AVL树的比较
    1.AVL树的时间复杂度虽然优于红黑树，但是对于现在的计算机，cpu太快，可以忽略性能差异
    2.红黑树的插入删除比AVL树更便于控制操作
    3.红黑树整体性能略优于AVL树(红黑树旋转情况少于AVL树)
  - 用法最广：Java ConcurrentHashMap & TreeMap；C++ STL: map & set；linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块；epoll在内核中的实现，用红黑树管理事件块；nginx中，用红黑树管理timer等
- 哈夫曼树：哈夫曼又称最优二叉树。是一种带权路径长度最短的二叉树，一般可以按下面步骤构建:
  - （1）将所有左，右子树都为空的作为根节点。（2）在森林中选出两棵根节点的权值最小的树作为一棵新树的左，右子树，置新树的附加根节点的权值为其左，右子树上根节点的权值之和。注意，左子树的权值应小于右子树的。（3）从森林中删除这两棵树，同时把新树加入到森林中。
  - （4）重复（2）（3）步骤，直到森林中只有一棵树为止，此树便是哈夫曼树。
多路查找树
- B 树：是一种自平衡的树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数时间内完成。B树，概括来说是一种自平衡的m阶树，与自平衡二叉查找树不同，B树适用于读写相对大的数据块的存储系统。
  - 根结点至少有两个子女。
  - 每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m
  - 每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m
  - 所有的叶子结点都位于同一层。
  - 每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。
    B-Tree中的每个节点根据实际情况可以包含大量的关键字信息和分支，如下图所示为一个3阶的B-Tree:
- B+ 树：B+ 树是一种树数据结构，通常用于关系型数据库(如Mysql)和操作系统的文件系统中。
  - B+ 树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。自底向上插入，与二叉树相反。
  - 在B树基础上，为叶子结点增加链表指针(B树+叶子有序链表)，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中。
  - b+树的非叶子节点不保存数据，只保存子树的临界值(最大或者最小)，所以同样大小的节点，b+树相对于b树能够有更多的分支，使得这棵树更加矮胖，查询时做的IO操作次数也更少。
    将上一节中的B-Tree优化，由于B+Tree的非叶子节点只存储键值信息，假设每个磁盘块能存储4个键值及指针信息，则变成B+Tree后其结构如下图所示:
- B* 树
- R 树：R树是用来做空间数据存储的树状数据结构。例如给地理位置，矩形和多边形这类多维数据建立索引。

避免孤立的学习知识点，要关联学习。

比如实际应用当中，我们经常使用的是查找和排序操作，这在我们的各种管理系统、数据库系统、操作系统等当中，十分常用，我们通过这个线索将知识点串联起来：
数组的下标寻址十分迅速，但计算机的内存是有限的，故数组的长度也是有限的；而且无序数组的查找最坏情况需要遍历整个数组；后来人们提出了二分查找，要求数组的构造一定有序，二分法查找解决了普通数组查找复杂度过高的问题。任何一种数组无法解决的问题就是插入、删除操作比较复杂，因此，在一个增删查改比较频繁的数据结构中，数组不会被优先考虑
普通链表由于它的结构特点被证明根本不适合进行查找
哈希表是数组和链表的折中，同时它的设计依赖散列函数的设计，数组不能无限长、链表也不适合查找，所以也不适合大规模的查找 ??? ???
二叉查找树因为可能退化成链表，同样不适合进行查找
AVL树是为了解决可能退化成链表问题，但是AVL树的旋转过程非常麻烦，因此插入和删除很慢，也就是构建AVL树比较麻烦
红黑树是平衡二叉树和AVL树的折中，是比较合适的。集合类中的Map、关联数组具有较高的查询效率，它们的底层实现就是红黑树。
多路查找树 是大规模数据存储中，实现索引查询这样一个实际背景下，树节点存储的元素数量是有限的(如果元素数量非常多的话，查找就退化成节点内部的线性查找了)，这样导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁，进而导致查询效率低下。
B树与自平衡二叉查找树不同，B树适用于读写相对大的数据块的存储系统，例如磁盘。它的应用是文件系统及部分非关系型数据库索引。
B+树在B树基础上，为叶子结点增加链表指针(B树+叶子有序链表)，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中。通常用于关系型数据库(如Mysql)和操作系统的文件系统中。
B* 树是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针, 在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3。
R树是用来做空间数据存储的树状数据结构。例如给地理位置，矩形和多边形这类多维数据建立索引。Trie树是自然语言处理中最常用的数据结构，很多字符串处理任务都会用到。
Trie树本身是一种有限状态自动机，还有很多变体。什么模式匹配、正则表达式，都与这有关。与树类似，用于处理字符串相关的问题时非常高效,它可以实现快速检索，常用于字典中的单词查询，搜索引擎的自动补全甚至 IP 路由。下图展示了“top”, “thus”和“their”三个单词在前缀树中如何存储的：
针对大量数据，如果在内存中作业优先考虑红黑树(map,set之类多为RB-tree实现)，如果在硬盘中作业优先考虑B系列树

各树详解：https://pdai.tech/md/algorithm/alg-basic-tree-search.html

二叉树

在Java中，二叉树是一种常见的树形数据结构，每个节点最多有两个子节点，分别为左子节点和右子节点。二叉树的节点类似于一个结构体，包含了数据、左子节点和右子节点的引用。以下是一个简单的二叉树的实现示例：

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int val) {   this.val = val;    this.left = null;    this.right = null;   }
}

public class BinaryTree {
    private TreeNode root;
    public BinaryTree() {    root = null;   }

    // 插入节点
    public void insert(int val) {
        root = insertRec(root, val);
    }
    private TreeNode insertRec(TreeNode root, int val) {
        if (root == null) {
            root = new TreeNode(val);
            return root;
        }
        if (val < root.val) {
            root.left = insertRec(root.left, val);
        } else if (val > root.val) {
            root.right = insertRec(root.right, val);
        }
        return root;
    }
    // 其他操作（搜索节点、删除节点等）可以根据需要实现
}

红黑树

红黑树的特性
（1）每个节点或者是黑色，或者是红色。
（2）根节点是黑色。
（3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL 或NULL)的叶子节点！ ]
（4）如果一个节点是红色的，则它的子节点必须是黑色的。
（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
左旋
对 x 进行左旋，意味着，将“x 的右孩子”设为“x 的父亲节点”；即，将 x 变成了一个左节点(x成了为 z 的左孩子)！因此，左旋中的“左”，意味着“被旋转的节点将变成一个左节点”。
右旋
对 x 进行右旋，意味着，将“x 的左孩子”设为“x 的父亲节点”；即，将 x 变成了一个右节点(x成了为 y 的右孩子)！因此，右旋中的“右”，意味着“被旋转的节点将变成一个右节点”。
添加
第一步: 将红黑树当作一颗二叉查找树，将节点插入。
第二步：将插入的节点着色为”红色”。
根据被插入节点的父节点的情况，可以将”当节点 z 被着色为红色节点，并插入二叉树”划分为三种情况来处理。
① 情况说明：被插入的节点是根节点。处理方法：直接把此节点涂为黑色。
② 情况说明：被插入的节点的父节点是黑色。处理方法：什么也不需要做。节点被插入后，仍然是红黑树。
③ 情况说明：被插入的节点的父节点是红色。这种情况下，被插入节点是一定存在非空祖父节点的；进一步的讲，被插入节点也一定存在叔叔节点(即使叔叔节点为空，我们也视之为存在，空节点本身就是黑色节点)。理解这点之后，我们依据”叔叔节点的情况”，将这种情况进一步划分为 3种情况(Case)
，，，
第三步: 通过一系列的旋转或着色等操作，使之重新成为一颗红黑树。
删除
第一步：将红黑树当作一颗二叉查找树，将节点删除。这和”删除常规二叉查找树中删除节点的方法是一样的”。分 3 种情况：
① 被删除节点没有儿子，即为叶节点。那么，直接将该节点删除就 OK 了。
② 被删除节点只有一个儿子。那么，直接删除该节点，并用该节点的唯一子节点顶替它的位置。
③ 被删除节点有两个儿子。那么，先找出它的后继节点；然后把“它的后继节点的内容”复制给“该节点的内容”；之后，删除“它的后继节点”。
第二步：通过”旋转和重新着色”等一系列来修正该树，使之重新成为一棵红黑树。因为”第一步”中删除节点之后，可能会违背红黑树的特性。所以需要通过”旋转和重新着色”来修正该树，使之重新成为一棵红黑树。
选择重着色 3 种情况。
① 情况说明： x 是“红+黑”节点。处理方法：直接把 x 设为黑色，结束。此时红黑树性质全部恢复。
② 情况说明： x 是“黑+黑”节点，且 x 是根。处理方法：什么都不做，结束。此时红黑树性质全部恢复。
③ 情况说明： x 是“黑+黑”节点，且 x 不是根。处理方法：这种情况又可以划分为 4 种子情况。这 4 种子情况如下表所示：
，，，，

B树

B-tree 又叫平衡多路查找树。一棵 m 阶的 B-tree (m 叉树)的特性如下（其中 ceil(x)是一个取上限的函数）：

树中每个结点至多有 m 个孩子；
除根结点和叶子结点外，其它每个结点至少有有 ceil(m / 2)个孩子；
若根结点不是叶子结点，则至少有 2 个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；
所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部结点或查询失败的结点，实际上这些结点不存在，指向这些结点的指针都为 null)；
每个非终端结点中包含有 n 个关键字信息： (n， P0， K1， P1， K2， P2， ……， Kn， Pn)。其中：
- Ki (i=1…n)为关键字，且关键字按顺序排序 K(i-1)< Ki。
- Pi 为指向子树根的接点，且指针 P(i-1)指向子树种所有结点的关键字均小于 Ki，但都大于 K(i-1)。
- 关键字的个数 n 必须满足： ceil(m / 2)-1 <= n <= m-1。

一棵 m 阶的 B+tree 和 m 阶的 B-tree 的差异在于：

有 n 棵子树的结点中含有 n 个关键字； (B-tree 是 n 棵子树有 n-1 个关键字)
所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。 (B-tree 的叶子节点并没有包括全部需要查找的信息)
所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。(B-tree 的非终节点也包含需要查找的有效信息)

位图

位图的原理就是用一个 bit 来标识一个数字是否存在，采用一个 bit 来存储一个数据，所以这样可以大大的节省空间。 bitmap 是很常用的数据结构，比如用于 Bloom Filter 中；用于无重复整数的排序等等。 bitmap 通常基于数组来实现，数组中每个元素可以看成是一系列二进制数，所有元素组成更大的二进制集合。

图

图(Graph)是由顶点和连接顶点的边构成的离散结构。图是最灵活的数据结构之一，很多问题都可以使用图模型进行建模求解。
理解：图基础，图的遍历，最小生成树(Prim & Kruskal)，最短路径(Dijkstra & Frolyd)，拓扑排序(Topological sort)，AOE & 关键路径等。

图的定义：图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为: G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。和线性表，树的差异:
- 线性表中我们把数据元素叫元素，树中将数据元素叫结点，在图中数据元素，我们则称之为顶点(Vertex)。
- 线性表可以没有元素，称为空表；树中可以没有节点，称为空树；但是，在图中不允许没有顶点(有穷非空性)。
- 线性表中的各元素是线性关系，树中的各元素是层次关系，而图中各顶点的关系是用边来表示(边集可以为空)
相关术语
- 顶点的度：顶点Vi的度(Degree)是指在图中与Vi相关联的边的条数。对于有向图来说，有入度(In-degree)和出度(Out-degree)之分，有向图顶点的度等于该顶点的入度和出度之和。
- 邻接：若无向图中的两个顶点V1和V2存在一条边(V1,V2)，则称顶点V1和V2邻接(Adjacent)；若有向图中存在一条边<V3,V2>，则称顶点V3与顶点V2邻接，且是V3邻接到V2或V2邻接直V3；
- 路径：在无向图中，若从顶点Vi出发有一组边可到达顶点Vj，则称该顶点序列为从顶点Vi到顶点Vj的路径(Path)。
- 连通：若从Vi到Vj有路径可通，则称顶点Vi和顶点Vj是连通(Connected)的。
- 权(Weight)：有些图的边或弧具有与它相关的数字，这种与图的边或弧相关的数叫做权(Weight)。
类型
- 无向图：如果图中任意两个顶点之间的边都是无向边(没有方向的边)，则称该图为无向图。边使用小括号“()”表示;如 (V1,V2);
- 有向图：如果图中任意两个顶点之间的边都是有向边(有方向的边)，则称该图为有向图。边使用尖括号“<>”表示;如 <V1,V2>
- 无向完全图: 在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。(有(n*(n-1))/2条边)
- 有向完全图: 在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。(含有n个顶点的有向完全图有n*(n-1)条边)
图的存储结构
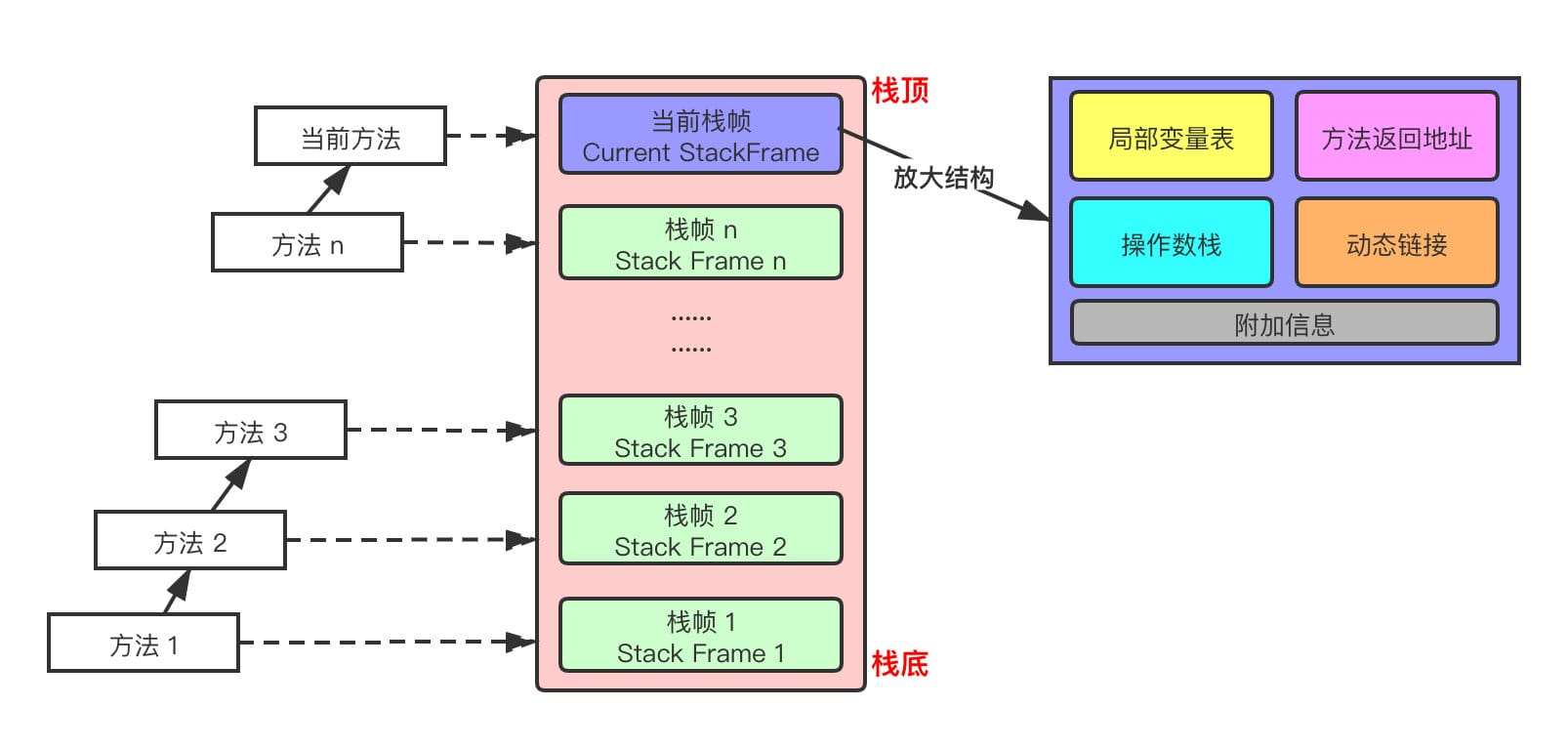
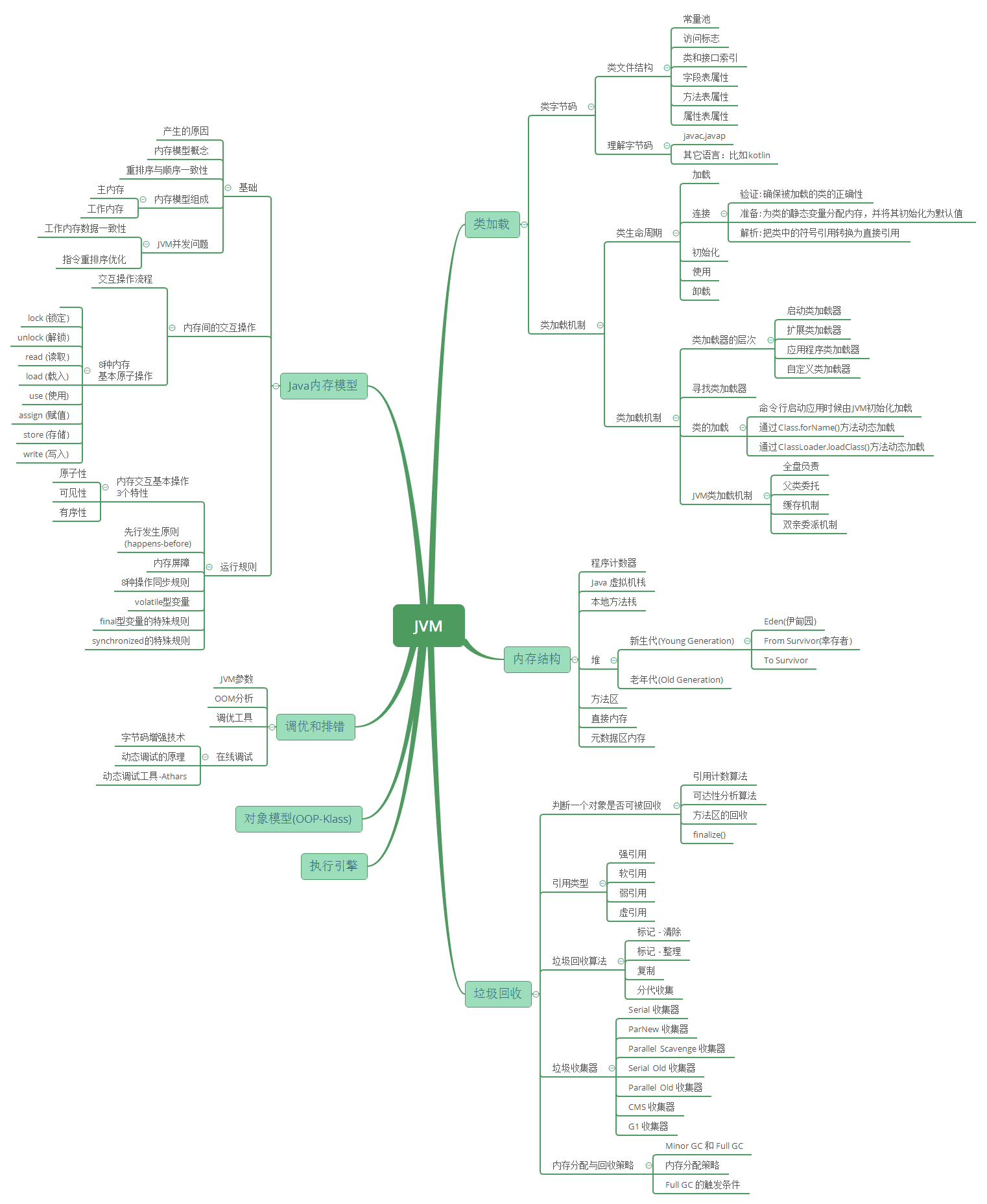
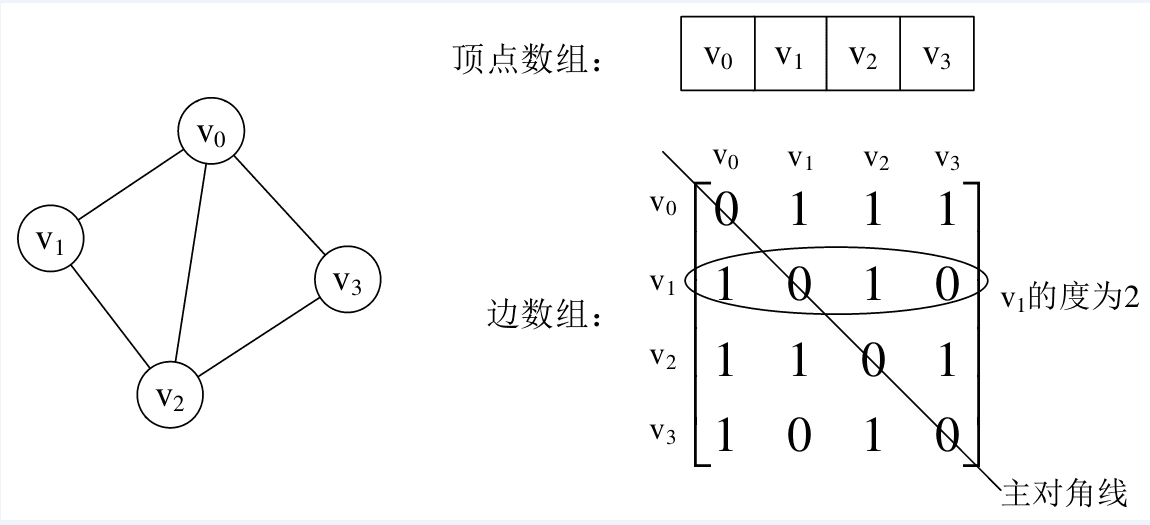
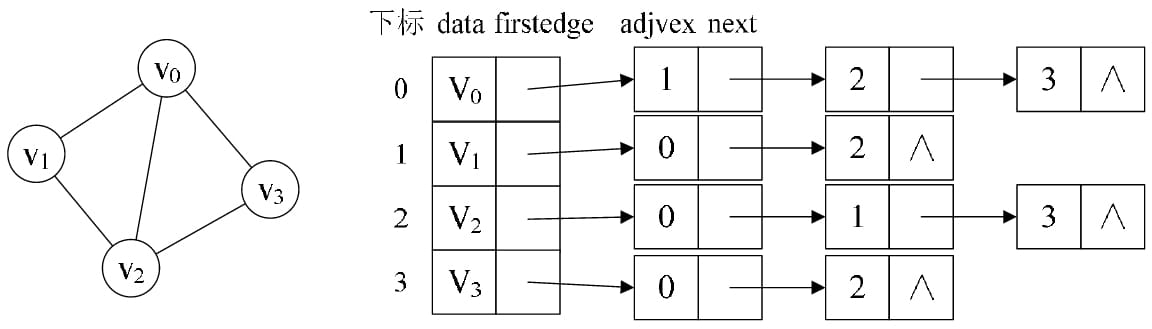
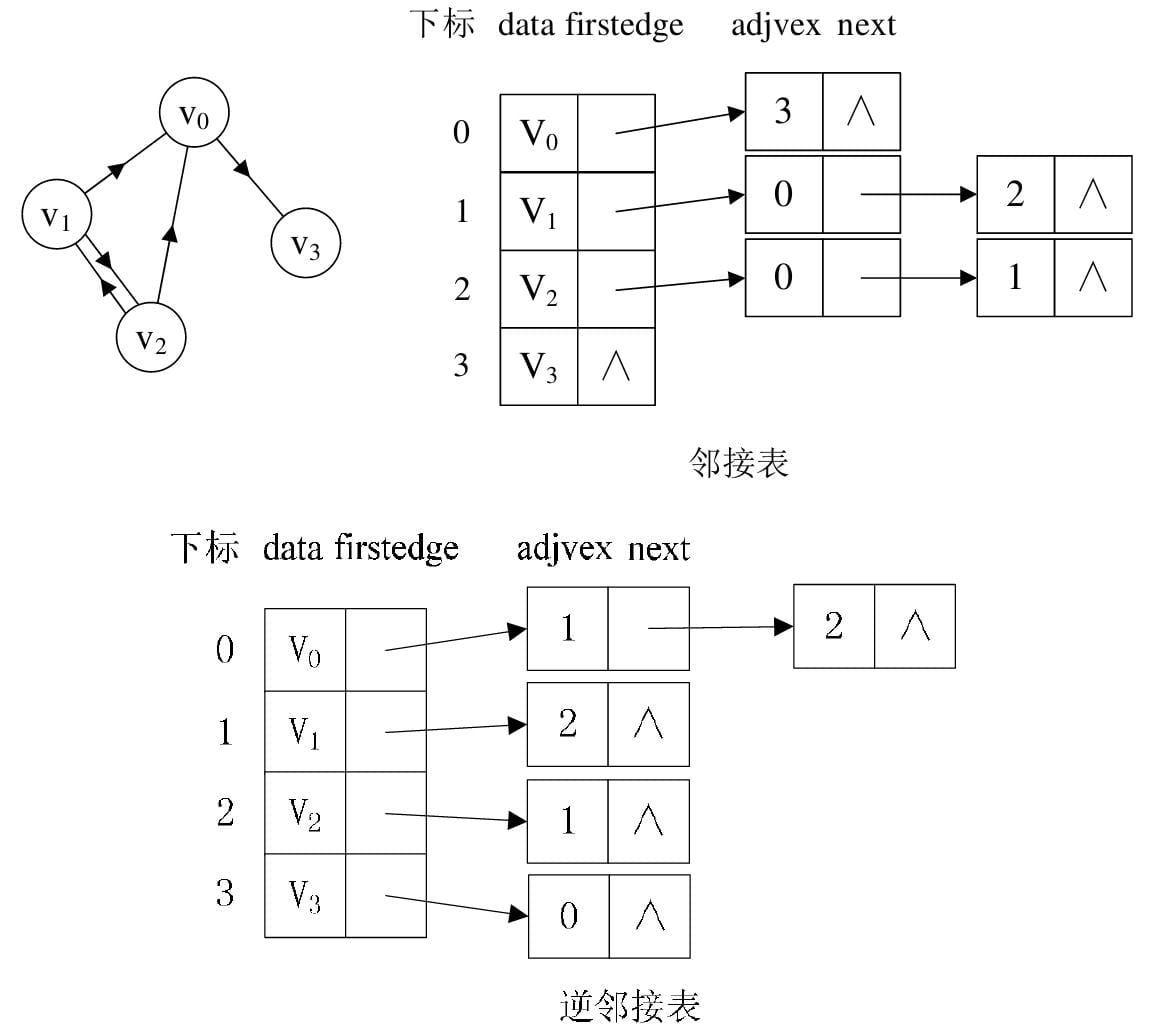
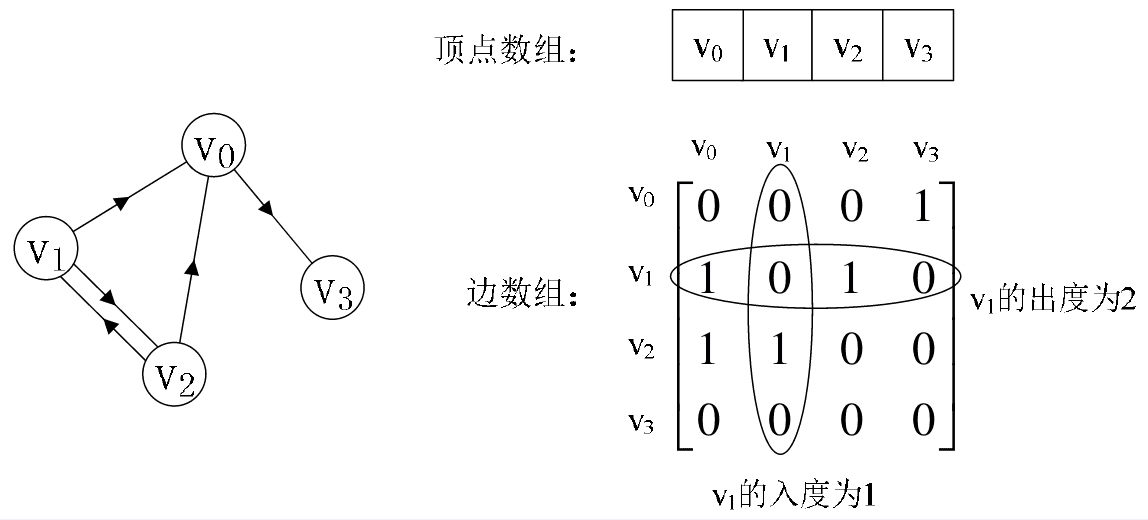- 邻接矩阵表示法：用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。不足: 由于存在n个顶点的图需要n*n个数组元素进行存储，当图为稀疏图时，使用邻接矩阵存储方法将会出现大量0元素，这会造成极大的空间浪费。这时，可以考虑使用邻接表表示法来存储图中的数据
- 邻接表表示法：邻接表由表头节点和表节点两部分组成，图中每个顶点均对应一个存储在数组中的表头节点。如果这个表头节点所对应的顶点存在邻接节点，则把邻接节点依次存放于表头节点所指向的单向链表中。

DFS

深度优先搜索: 假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。显然，深度优先搜索是一个递归的过程。

void dfs(vexnode *g[], int v1) {
    stack<vexnode*> stk;
    stk.push(g[v1]);
    g[v1]->visited = true;
    while (!stk.empty()) {
        vexnode *cur = stk.top();
        stk.pop();
        cout << cur->val << " ";
        for (vexnode *neighbor : cur->neighbors) {
            if (!neighbor->visited) {
                neighbor->visited = true;
                stk.push(neighbor);
            }
        }
    }
}

BFS

广度优先搜索算法(Breadth First Search)，又称为”宽度优先搜索”或”横向优先搜索”。
它的思想是: 从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。
换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远，依次访问和v有路径相通且路径长度为1,2…的顶点。

void bfs(vexnode *g[], int v1) {
    queue<vexnode*> que;
    que.push(g[v1]);
    g[v1]->visited = true;

    while (!que.empty()) {
        vexnode *cur = que.front();
        que.pop();
        cout << cur->val << " ";

        for (vexnode *neighbor : cur->neighbors) {
            if (!neighbor->visited) {
                neighbor->visited = true;
                que.push(neighbor);
            }
        }
    }
}

DFS & BFS 实现 https://pdai.tech/md/algorithm/alg-basic-graph-bfs-dfs.html

ACM模式Java输入

核心代码模式下不用考虑输入输出的问题，只需要根据所给函数框架写中间逻辑代码。但是在ACM模式下要，即函数的输入是从控制台键入的几行数据，而输出是直接将结果打印到控制台。
nextInt()：直至读取到空格或回车之后结束本次的int值；
next()：直至读取到空格或回车之后结束本次的String值，不可读取回车；
nextLine()：直至读取到换行符（回车）之后结束本次读取的String，可读取回车（空值）

单个输入

有的函数输入很简单，就是一个数，或者一个字符串，或者一行数中间用空格隔开，这种输入很简单，处理方法如下。

import java.util.Scanner;

public class test{
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        // 读取输入的一个整型
        int n = sc.nextInt();
        // 如果输入的是double类型
        double d = sc.nextDouble();
        // 如果输入的是一个字符串
        String s = sc.next(); 
        // 读取的是一整行
        String l = sc.nextLine(); 
    }
}

一行输入

如果输入的是一行数据，中间用空格隔开，比如输入的是2 3 4

Scanner sc = new Scanner(System.in);
int n1 = sc.nextInt();  // 接收第1个数
int n2 = sc.nextInt();	// 接收第2个数
int n3 = sc.nextInt();	// 接收第3个数

有时候输入不是空格分隔，而是逗号分割的，比如输入的是1,2,3,4,5，并假设我们需要用数组接收，可以这么操作

Scanner sc = new Scanner(System.in);
//以字符串形式作为输入
String str = sc.next();
//通过分隔符将其转为字符串数组
String[] arr = str.split(",");
//初始化一个整数数组
int[] nums = new int[arr.length];
//给整数数组赋值
for (int j = 0; j < nums.length; j++) {
    nums[j] = Integer.parseInt(arr[j]);
}

多行输入

一共输入两行，第一行表示第二行有多少个数，比如第一行为4，第二行为0 2 3 4。

Scanner sc = new Scanner(System.in);
// 第一行的数表示第二行有多少个数，即数组的长度
int n = sc.nextInt();
int[] nums = new int[n];
for (int i = 0; i < n; i++) {
    nums[i] = sc.nextInt();
}

持续输入

如果题目中没有明说一次给几个输入，为了保险可以直接无脑用 while(sc.hasNext()) {} 包括起来，一直等待输入，除非终止程序。

while (sc.hasNext()) {
    String str = sc.nextLine();
    // 多个输入都需要经过相同的逻辑判断然后在输出
}

Acm模式输出

System.out.print();   // 用于打印不带换行符的内容到控制台
System.out.println(); // 用于打印带换行符的内容到控制台，打印完后会换行
System.out.format();  // 用于格式化输出，可以通过格式化字符串来指定输出的格式
System.out.printf();  // 也用于格式化输出，但是使用更简单，格式化字符串以及对应的参数放在一起即可
System.out.println("Hello" + ", " + "world" + "!"); // 字符串连接可以直接用 + 号："Hello, world!"

// 规格化的输出：
// `#` 表示如果该位置有数字则显示，否则不显示；`0` 表示该位置无论是否有数字都显示，如果没有数字则显示 `0`；
DecimalFormat fd = new DecimalFormat("#.00#");
DecimalFormat gd = new DecimalFormat("0.000");
System.out.println("x =" + fd.format(x)); // `.00#` 表示保留两位小数并四舍五入；x = 12.3456， fd.format(x) 输出的结果是 12.35
System.out.println("x =" + gd.format(x)); // `0.000` 表示保留三位小数四舍五入； x = 12.3456， gd.format(x) 输出的结果是 12.346

1
2
3

// 二进制字符串输出：
String binaryString = Integer.toBinaryString(42); // 将整数转换为二进制字符串
System.out.println("Binary representation of " + number + " is: " + binaryString);

日期处理

SimpleDateFormat 用于日期格式化和解析，可以将日期对象格式化为指定的字符串，也可以将特定格式的字符串解析为日期对象。

格式化日期为字符串：

1
2
3

SimpleDateFormat sdf = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
Date now = new Date();
String formattedDate = sdf.format(now);

解析字符串为日期：

SimpleDateFormat sdf = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
String dateString = "2024-03-02 15:30:00";
Date parsedDate = sdf.parse(dateString);
System.out.println("Parsed Date: " + parsedDate);

文件读写

我们读取 a.txt 和 b.txt 中的内容，并将其写入到 c.txt 中。然后，我们统计总行数并在第一行写入总行数。
请注意，在写入总行数之前需要先将文件关闭并重新打开以实现在文件的开头插入内容。

public class FileCopyWithLineCount {
    public static void main(String[] args) {

        try (
            BufferedReader reader1 = new BufferedReader(new FileReader("a.txt"));
            BufferedReader reader2 = new BufferedReader(new FileReader("b.txt"));
            BufferedWriter writer = new BufferedWriter(new FileWriter("c.txt"))
        ) {
            // 读取第一个文件并写入到输出文件
            String line;
            int totalCount = 0;
            while ((line = reader1.readLine()) != null) {
                writer.write(line);
                writer.newLine();
                totalCount++;
            }

            // 读取第二个文件并写入到输出文件
            while ((line = reader2.readLine()) != null) {
                writer.write(line);
                writer.newLine();
                totalCount++;
            }

            // 在第一行写入总行数
            writer.flush();
            writer.close();
            BufferedWriter writer2 = new BufferedWriter(new FileWriter("c.txt", true));
            writer2.write("Total Lines: " + totalCount);
            writer2.newLine();
            writer2.flush();
            writer2.close();

            System.out.println("内容已成功从 " + "a.txt" + " 和 " + "b.txt" + " 读取并写入 " + "c.txt");
        } catch (IOException e) {
            System.err.println("发生IO异常: " + e.getMessage());
        }
    }
}

位运算

Java 中的位运算是对二进制数据进行操作的一种方式，常用的位运算符有以下几种：

按位与（&）：两个位都为 1 时，结果为 1；否则为 0。例如：1010 & 1100 = 1000。
按位或（|）：两个位中至少有一个为 1 时，结果为 1；否则为 0。例如：1010 | 1100 = 1110。
按位异或（^）：两个位相同为 0，不同为 1。例如：1010 ^ 1100 = 0110。
按位取反（~）：对一个二进制数的每个位取反，0 变为 1，1 变为 0。例如：~1010 = 0101。
左移（<<）：将一个数的所有位向左移动指定的位数，右侧空出的位用 0 填充。例如：1010 << 2 = 101000。
右移（>>）：将一个数的所有位向右移动指定的位数，左侧空出的位用符号位填充（正数用 0，负数用 1）。例如：1010 >> 2 = 10。
无符号右移（>>>）：将一个数的所有位向右移动指定的位数，左侧空出的位用 0 填充。例如：1010 >>> 2 = 10。

时间复杂度

时间复杂度是一种用来衡量算法运行时间与输入规模之间关系的概念。它不是用来精确测量程序运行时间的，而是描述在输入规模变化时，算法运行时间的增长趋势。
大O表示上界，当用它作为算法的最坏情况运行时间的上界，就是对任意数据输入的运行时间的上界。
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!)

♥常见排序算法知识体系详解♥

A. 重点理解几个排序之间的对比，时间和空间复杂度，以及应用。PS：越简单越要提高认知效率，做到战略上藐视战术上重视。
B. 具体分析各种排序及其复杂度，查漏补缺；在综合复杂度及稳定性情况下，通常希尔, 快排和归并需要重点掌握。
稳定性：指相等元素的相对顺序在排序前后是否保持不变。稳定性在某些应用场景中很重要，例如在对相同优先级的任务进行排序时，保持原始顺序可确保任务的处理顺序不被打乱。

https://leo710aka.github.io/2020/09/09/5%20%E7%B4%A2%E5%BC%95_%E6%8E%92%E5%BA%8F_/

冒泡排序(Bubble Sort)
它是一种较简单的排序算法。它会遍历若干次要排序的数列，每次遍历时，它都会从前往后依次的比较相邻两个数的大小；如果前者比后者大，则交换它们的位置。这样，一次遍历之后，最大的元素就在数列的末尾！采用相同的方法再次遍历时，第二大的元素就被排列在最大元素之前。重复此操作，直到整个数列都有序为止

public static void bubbleSort1(int [] a, int n){
    int i, j;
    for(i=0; i<n; i++){//表示 n 次排序过程。
        for(j=1; j<n-i; j++){
            if(a[j-1] > a[j]){//前面的数字大于后面的数字就交换
                //交换 a[j-1]和 a[j]
                int temp;
                temp = a[j-1];
                a[j-1] = a[j];
                a[j]=temp;
            }
        }
    }
}

插入排序(Insertion Sort)
基本思想是: 把n个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含1个元素，无序表中包含有n-1个元素，排序过程中每次从无序表中取出第一个元素，将它插入到有序表中的适当位置，使之成为新的有序表，重复n-1次可完成排序过程。

public void sort(int arr[]){
    for(int i = 1; i < arr.length; i++) {
        // 插入的数
        int insertVal = arr[i];
        // 被插入的位置(准备和前一个数比较)
        int index = i - 1;
        // 如果插入的数比被插入的数小
        while(index >= 0 && insertVal < arr[index]) {
            // 将把 arr[index] 向后移动
            arr[index+1] = arr[index];
            // 让 index 向前移动
            index--;
        }
        // 把插入的数放入合适位置
        arr[index+1] = insertVal;
        }
    }

选择排序(Selection sort)
基本思想是: 首先在未排序的数列中找到最小(or最大)元素，然后将其存放到数列的起始位置；接着，再从剩余未排序的元素中继续寻找最小(or最大)元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

void SelectionSort(int a[], int len) {
	for (int i = 0; i < len - 1; i++) { 
		int minIndex = i;
		for (int j = i + 1; j <len; j++) {
			if(a[j] < a[minIndex]) {
				minIndex = j;
			}
		}
		swap(a[i], a[minIndex]);
	}
}

快速排序(Quick Sort)
采用分治的思想，将一个数组分成两个子数组，然后递归地对子数组进行排序。它选择一个元素作为”pivot”（基准），并将数组中小于基准的元素放在基准的左边，大于基准的元素放在基准的右边，然后对左右子数组进行递归排序。

public void quickSort(int[] nums, int low, int high) {
    if (low >= high) return; // 边界条件判断
    int start = low;
    int end = high;
    int key = nums[low];
    while (end > start) {
        while (end > start && nums[end] >= key) {
            end--;
        }
        if (end > start) {
            nums[start] = nums[end];
        }
        while (end > start && nums[start] <= key) {
            start++;
        }
        if (end > start) {
            nums[end] = nums[start];
        }
    }
    nums[start] = key; // 基准值放回合适位置
    quickSort(nums, low, start - 1); // 左边序列递归排序
    quickSort(nums, start + 1, high); // 右边序列递归排序
}

希尔排序(Shell Sort)：实质上是一种分组插入方法。
它的基本思想是: 对于n个待排序的数列，取一个小于n的整数gap(gap被称为步长)将待排序元素分成若干个组子序列，所有距离为gap的倍数的记录放在同一个组中；然后，对各组内的元素进行直接插入排序。这一趟排序完成之后，每一个组的元素都是有序的。然后减小gap的值，并重复执行上述的分组和排序。重复这样的操作，当gap=1时，整个数列就是有序的。

private void shellSort(int[] a) {
    int dk = a.length/2;
    while( dk >= 1 ){
        ShellInsertSort(a, dk);
        dk = dk/2;
    }
}
private void ShellInsertSort(int[] a, int dk) {
    //类似插入排序，只是插入排序增量是 1，这里增量是 dk,把 1 换成 dk 就可以了
    for(int i=dk;i<a.length;i++){
        if(a[i]<a[i-dk]){
            int j;
            int x=a[i];//x 为待插入元素
            a[i]=a[i-dk];
            for(j=i-dk; j>=0 && x<a[j];j=j-dk){
                //通过循环，逐个后移一位找到要插入的位置。
                a[j+dk]=a[j];
            }
            a[j+dk]=x;//插入
        }
    }
}

堆排序(Heap Sort)

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。
它具有 O(n log n) 的时间复杂度，并且是原地排序算法（不需要额外的空间）。堆排序分为两个阶段：建堆和排序。
1. 建堆（Heapify）：
  - 将待排序数组视为完全二叉树，从最后一个非叶子节点开始，依次向上进行调整，使得每个节点都满足堆的性质（最大堆或最小堆）。
  - 对于最大堆，父节点的值大于或等于子节点的值；对于最小堆，父节点的值小于或等于子节点的值。
  - 建堆过程可以通过自上而下的调整（向下调整）或自下而上的调整（向上调整）来实现。
2. 排序：
  - 将堆顶元素（根节点）与最后一个元素交换，并将最后一个元素移出堆（视为已排序部分）。
  - 对剩余的元素重新进行堆调整，使得剩余元素重新构成堆。
  - 重复上述步骤，直到所有元素都被移出堆，完成排序。
下面是堆排序的详细步骤：
1. 将待排序数组构建成一个最大堆（或最小堆），即建堆过程。可以选择自上而下的调整（向下调整）或自下而上的调整（向上调整）来实现。
2. 从最后一个非叶子节点开始，依次向前对每个节点进行堆调整，使得当前节点及其子树满足堆的性质。
3. 交换堆顶元素（根节点）和最后一个元素，并将最后一个元素移出堆（视为已排序部分）。
4. 对剩余的元素重新进行堆调整，使得剩余元素重新构成堆。
5. 重复步骤3和步骤4，直到所有元素都被移出堆，完成排序。

void AdjustDwon(int* a, int size, int parent){
    int child = parent * 2 + 1;
    while (child < size) {
        if (child + 1 < size && a[child + 1] > a[child]) {
            ++child;
        }
        if (a[child] > a[parent]) {
            swap(a[child], a[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else {
            break;
        }
    }
}
void HeapSort(int* a, int n){
    for (int i = (n - 1 - 1) / 2; i >= 0; i--) {
        AdjustDwon(a, n, i);
    }
    int end = n - 1;
    while (end > 0)	{
        swap(a[0], a[end]);
        AdjustDwon(a, end, 0);
        --end;
    }
}

桶排序：原理很简单，将数组分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）

public static void bucketSort(int[] arr){
    int max = Integer.MIN_VALUE;
    int min = Integer.MAX_VALUE;
    for(int i = 0; i < arr.length; i++){
        max = Math.max(max, arr[i]);
        min = Math.min(min, arr[i]);
    }
    //创建桶
    int bucketNum = (max - min) / arr.length + 1;
    ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
    for(int i = 0; i < bucketNum; i++){
        bucketArr.add(new ArrayList<Integer>());
    }
    //将每个元素放入桶
    for(int i = 0; i < arr.length; i++){
        int num = (arr[i] - min) / (arr.length);
        bucketArr.get(num).add(arr[i]);
    }
    //对每个桶进行排序
    for(int i = 0; i < bucketArr.size(); i++){
        Collections.sort(bucketArr.get(i));
    }
}

归并排序算法：采用分治的思想将一个大问题分割成多个小问题来解决。
具体来说，归并排序的过程包括分割、排序和合并三个步骤。

void merge(vector<int>& arr, int left, int mid, int right) {
    int n1 = mid - left + 1, n2 = right - mid;
    vector<int> leftArr(n1), rightArr(n2);                        // 创建临时数组来存储左右两部分的数据
    for (int i = 0; i < n1; i++)  leftArr[i] = arr[left + i];     // 将数据复制到临时数组
    for (int i = 0; i < n2; i++)  rightArr[i] = arr[mid + 1 + i];    
    int i = 0, j = 0, k = left;                                   // 合并两个临时数组
    while (i < n1 && j < n2) {
        if (leftArr[i] <= rightArr[j]) arr[k++] = leftArr[i++];  
        else arr[k++] = rightArr[j++]; 
    }
    while (i < n1)  arr[k++] = leftArr[i++];                      // 处理剩余元素
    while (j < n2)  arr[k++] = rightArr[j++];  
}
void mergeSort(vector<int>& arr, int left, int right) {           // 归并排序主函数
    if (left < right) {
        int mid = left + (right - left) / 2;
        mergeSort(arr, left, mid);                                // 分割左右两部分
        mergeSort(arr, mid + 1, right); 
        merge(arr, left, mid, right);                             // 合并已排序的两部分
    }
}

基数排序
基本思想是: 将整数按位数切割成不同的数字，然后按每个位数分别比较。具体做法是: 将所有待比较数值统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列

public class radixSort {
    int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,101,56,17,18,23,34,15,35,2 5,53,51};
    public radixSort(){
        sort(a);
        for(inti=0;i<a.length;i++){
            System.out.println(a[i]);
        }
    }
    public void sort(int[] array){
        //首先确定排序的趟数;
        int max=array[0];
        for(inti=1;i<array.length;i++){
            if(array[i]>max){
                max=array[i];
            }
        }
        int time=0;
        //判断位数;
        while(max>0){
            max/=10;
            time++;
        }
        //建立 10 个队列;
        List<ArrayList> queue=newArrayList<ArrayList>();
        for(int i=0;i<10;i++){
            ArrayList<Integer>queue1=new ArrayList<Integer>();
            queue.add(queue1);
        }
        //进行 time 次分配和收集;
        for(int i=0;i<time;i++){
            //分配数组元素;
            for(intj=0;j<array.length;j++){
                //得到数字的第 time+1 位数;
                int x=array[j]%(int)Math.pow(10,i+1)/(int)Math.pow(10, i);
                ArrayList<Integer>queue2=queue.get(x);
                queue2.add(array[j]);
                queue.set(x, queue2);
                }
                int count=0;//元素计数器;
                //收集队列元素;
                for(int k=0;k<10;k++){
                while(queue.get(k).size()>0){
                    ArrayList<Integer>queue3=queue.get(k);
                    array[count]=queue3.get(0);
                    queue3.remove(0);
                    count++;
                }
            }
        }
    }
}

2021-09-01

Java 基础

Java 是一种高级编程语言和计算平台。它最初由Sun（后被Oracle收购）于1995年发布，旨在实现“一次编写，到处运行”的理念。
Java SE（标准版）：是 Java 平台的基本版本，也是最基本的 Java 编程平台。提供了 Java 编程语言的核心功能，包括基本的语言结构、标准库、输入/输出、多线程支持等。Java SE 适用于通用的桌面应用程序、命令行工具、小型服务、移动应用程序等各种领域。
Java EE（企业版）：是在 Java SE 的基础上构建的，专门用于开发和运行企业级应用程序的平台。它提供了一组扩展和 API，用于构建大型、分布式、可伸缩、高性能的应用程序，如企业级 Web 应用、电子商务系统等。Java EE 包括了 Servlet、JSP、EJB、JPA等各种技术和规范，以支持不同类型的企业级应用。

Java 是由 Sun Microsystems 公司于 1995 年 5 月推出的高级程序设计语言。Java 可运行于多个平台，如 Windows, Mac OS 及其他多种 UNIX 版本的系统。
移动操作系统 Android 大部分的代码采用 Java 编程语言编程。

面向对象三大特性

封装

利用抽象数据类型将数据和基于数据的操作封装在一起，使其构成一个不可分割的独立实体。数据被保护在抽象数据类型的内部，尽可能地隐藏内部的细节，只保留一些对外接口使之与外部发生联系。用户无需知道对象内部的细节，但可以通过对象对外提供的接口来访问该对象。

继承

继承实现了 IS-A 关系，例如 Cat 和 Animal 就是一种 IS-A 关系，因此 Cat 可以继承自 Animal，从而获得 Animal 非 private 的属性和方法。继承应该遵循里氏替换原则，子类对象必须能够替换掉所有父类对象。Cat 可以当做 Animal 来使用，也就是说可以使用 Animal 引用 Cat 对象。父类引用指向子类对象称为向上转型。

1
2

// 向上继承是面向对象编程中的一个关键概念，它通过创建一个统一的接口和通用的父类，支持多态性，减少代码重复，提高
Animal animal = new Cat();  // 代码的可维护性和可扩展性。使代码更灵活、通用和易于理解，有助于构建更高质量的程序

多态

编译时多态主要指方法的重载（一个类中的多个同名方法）
运行时多态指程序中定义的对象引用所指向的具体类型在运行期间才确定（父,子类之间）；有三个条件:继承、覆盖(重写)、向上转型

public class Animal {                public void play() {  System.out.println("aoaoao.."); }}
public class Dog extends Animal {    public void play() {  System.out.println("旺旺旺");    }}
public class Cat extends Animal {    public void play() {  System.out.println("喵喵喵");    }}
public class Music {
    public static void main(String[] args) {
        List<Animal> animals = new ArrayList<>();
        animals.add(new Cat());  
        animals.add(new Dog());    // animals.add(new ..()).....
        for(Animal animal : animals) {            
            animal.play();        
        }    
    }
}

数据类型

数据类型定义了数据的种类和取值范围，以及对这些数据执行的操作。在Java中，数据类型主要分为两类：

1. 基本数据类型

基本数据类型：这些数据类型是Java语言的一部分，用于表示基本的数据值。有以下几种：
整数类型：byte、short、int、long; 浮点数类型：float、double; 字符类型：char; 布尔类型：boolean
Integer.MAX_VALUE常量表示int类型的最大值，值为2147483647。

类型 byte short int long float double char boolean

大小(Byte) 1 2 4 8 4 8 2 1
包装类型：包装是指将基本数据类型包装在对象中的过程。这是因为 Java 是面向对象的编程语言，需要将基本数据类型封装在对象中，从而在面向对象的上下文中使用它们，在处理集合、泛型、反射等Java编程中的许多场景中非常有用。例如，你可以将一个 int 存储在一个 List<Integer> 中，而不是 List<int>
类型对应：byte - Byte, short - Short, int - Integer, long - Long, float - Float, double - Double, char - Character, boolean - Boolean
1
2
Integer x = 2; // 装箱，基本类型与其对应的包装类型之间的赋值使用自动装箱与拆箱完成。
int y = x; // 拆箱

类型转换（char、String、int和double之间）

// int 转 double: int i = 123;
double d = (double)i; // 或者直接 d = i;
// double 转 int: double d = 123.45;
int i = (int)d; // 使用类型转换，但请注意这会截断小数部分。结果是 123

// int 转 char：int i = 97;
char c = (char)i;    // 通过 ASCII值转换。97 对应的字符是 'a'
c = (char)(c + 32);  // 大小写字母差值32，与cpp中的一样
// char 转 int：char c = 'a';
int i = (int)c; // 通过ASCII值转换。'a' 的ASCII值是 97
int j = '9' - '0';

// int 转 String
int number = 123;
String strNumber1 = String.valueOf(number);  
String strNumber2 = "" + number;            
String strNumber3 = Integer.toString(number); 
// String 转 int
int number = Integer.parseInt(str); // 默认十进制
int numBinary = Integer.parseInt(binaryStr, 2); // 二进制

// String 转 double: String doubleStr = "123.45";
double d = Double.parseDouble(doubleStr);
// double 转 String: double d = 123.45;
String str = String.valueOf(d); // 或者 "str = d +;"

// char 转 String：char c = 'a';
String str = Character.toString(c);
str += c; // 将 `char` 直接与字符串连接（`char` 会自动被转换成 `String`）。
// String 转 char：String str = "hello";
char c = Character.charAt(str, 0); // 获取字符串的第一个字符

2. 引用数据类型

引用数据类型用于引用对象，而不是直接存储数据值。引用数据类型包括类、接口、数组、枚举等。

引用：引用是一个变量，用于存储对象的内存地址。它指向对象在堆内存中的位置，而不是对象本身。通过引用，可以访问和操作对象的数据和方法。
引用类型：引用类型是Java中的数据类型之一，用于声明引用变量。Java的引用类型包括类、接口、数组、枚举和注解。引用类型的变量可以用来引用相应类型的对象。
堆内存：在Java中，所有的对象都存储在堆内存中。引用变量存储的是对象在堆内存中的地址。当创建一个新对象时，它被分配到堆内存中，然后引用变量被赋予该对象的地址。
栈内存：Java中的引用变量本身存储在栈内存中。栈内存用于存储局部变量，包括引用变量。引用变量在栈上分配内存，但它们指向的对象存储在堆内存中。
强引用：强引用是最常见的引用类型。当一个对象被强引用变量引用时，它不会被垃圾回收器回收，直到引用变量不再引用该对象。如果没有任何强引用指向一个对象，该对象就会成为垃圾，可以被垃圾回收。
软引用：软引用用于描述一些还有用但并非必需的对象。当内存不足时，垃圾回收器可能会回收被软引用引用的对象，释放内存。这可以防止内存溢出，但不会保证垃圾回收器什么时候回收这些对象。
弱引用：弱引用用于描述非必需对象的引用。弱引用的对象会在垃圾回收器下次运行时被回收，不论内存是否足够。这使得弱引用适用于临时对象和缓存。
虚引用：虚引用是最弱的引用类型。虚引用的对象没有直接访问的权限，它主要用于跟踪对象是否被回收。虚引用必须和引用队列（ReferenceQueue）一起使用，以便在对象被回收时收到通知。

主要引用类型:

类引用类型：类引用类型用于引用类的实例，即对象。这是Java中最常见的引用类型。例如，如果有一个类 Person，您可以创建 Person 类型的引用来引用不同的 Person 对象：Person person = new Person();
接口引用类型：接口引用类型用于引用实现了特定接口的对象。例如，如果有一个接口 Drawable，您可以创建 Drawable 类型的引用来引用实现了 Drawable 接口的对象：Drawable drawable = new Circle();
数组引用类型：数组引用类型用于引用数组对象。数组可以包含基本数据类型或引用类型的元素。例如，int[] numbers 是一个引用类型，用于引用整数数组。
枚举引用类型
泛型引用类型
父类引用类型：父类引用类型用于引用子类对象。这可以用于实现多态。例如，如果有一个父类 Animal 和一个子类 Dog，您可以创建 Animal 类型的引用来引用 Dog 对象：Animal animal = new Dog();

`Java中的引用`不是直接的内存地址，而是对实际对象的间接引用。这使得Java程序员不需要关心内存管理，因为Java虚拟机（JVM）会自动管理对象的创建和销毁。

与C++中的指针不同。Java中的引用是一种高级抽象，它隐藏了对象的底层内存地址和操作，使得程序员不需要关心内存管理。
Java中的引用本质上是一个抽象的句柄（handle），它不直接指向对象的内存地址，而是指向Java虚拟机（JVM）内部的数据结构，该数据结构包含了对象的信息以及对象在堆内存中的位置。这种抽象层级使Java更安全，因为程序员无法直接操纵内存地址，从而避免了许多常见的内存错误，如指针溢出和内存泄漏。

枚举类

Java中的枚举类是一种特殊的类，用于定义一组常量。枚举类可以包含字段、方法和构造函数。

定义简单的枚举类：

// 定义一个简单的枚举类
enum Day {
    MONDAY, TUESDAY, WEDNESDAY, THURSDAY, FRIDAY, SATURDAY, SUNDAY;
}
public class EnumExample {
    public static void main(String[] args) {
        // 使用枚举常量
        Day today = Day.MONDAY;
        System.out.println("Today is: " + today);
    }
}

枚举类包含字段和方法：

// 定义包含字段和方法的枚举类
enum Color {
    RED("#FF0000"), GREEN("#00FF00"), BLUE("#0000FF");
    private String hexCode;
    // 构造函数
    private Color(String hexCode) {
        this.hexCode = hexCode;
    }
    // 获取颜色的十六进制代码
    public String getHexCode() {
        return hexCode;
    }
}

public class EnumWithFieldsAndMethods {
    public static void main(String[] args) {
        // 使用枚举常量和方法
        Color color = Color.BLUE;
        System.out.println("Color is " + color + " with hex code " + color.getHexCode());
    }
}

Java中的枚举类可以包含抽象方法。在这种情况下，每个枚举常量都必须实现抽象方法。

// 定义带有抽象方法的枚举类
enum Operation {
    ADD {
        @Override
        public int apply(int x, int y) {
            return x + y;
        }
    },
    SUBTRACT {
        @Override
        public int apply(int x, int y) {
            return x - y;
        }
    },
    // 定义抽象方法
    public abstract int apply(int x, int y);
}

public class EnumWithAbstractMethod {
    public static void main(String[] args) {
        // 使用带有抽象方法的枚举
        int result = Operation.ADD.apply(5, 3);
        System.out.println("Result: " + result);
    }
}

String

String 被声明为 final，因此它不可被继承。内部使用 char 数组存储数据，该数组被声明为 final，这意味着 value 数组初始化之后就不能再引用其它数组。并且 String 内部没有改变 value 数组的方法，因此可以保证 String类不可变。

String Pool ：如果一个 String 对象已经被创建过了，那么就会从 String Pool 中取得引用。

String 不可变，StringBuffer 和 StringBuilder 可变。
String 不可变，因此是线程安全的，StringBuilder 不是线程安全的，StringBuffer 是线程安全的，内部使用 synchronized 进行同步

String s1 = new String("aaa");
String s2 = new String("aaa");
System.out.println(s1 == s2);           // false; s1 和 s2 采用 new String() 的方式新建了两个不同对象
String s3 = s1.intern();
System.out.println(s1.intern() == s3);  // true; s3 是通过 s1.intern() 方法 首先把 s1 引用的对象放到 String Pool(字符串常量池)中，然后返回这个对象引用。因此 s3 和 s1 引用的是同一个字符串常量池的对象
String s4 = "bbb";
String s5 = "bbb";
System.out.println(s4 == s5);           // true; 采用 "bbb" 这种使用双引号的形式创建字符串实例，会自动地将新建的对象放入 String Pool 中

Java 容器

容器：Java 容器就是可以容纳其他 Java 对象的对象。Java Collections Framework(JCF) 为开发者提供了通用的容器，始于JDK 1.2
- 优点: 降低编程难度，提高程序性能，提高API间的互操作性，降低设计和实现相关API的难度，增加程序的重用性
- 对于基本类型(int, long, float, double等)，需要将其包装成对象类型后(Integer, Long, Float, Double等)才能放到容器里。很多时候拆包装和解包装能够自动完成。这虽然会导致额外的性能和空间开销，但简化了设计和编程。
- 容器接口主要包括 Collection(容器类) 和 Map 两种，
  Collection 存储着对象的集合，而 Map 存储着键值对(两个对象)的映射表。

1. Collection

Set

主要功能是保证存储的集合不会重复，至于集体是有序还是无序的，需要看具体的实现类，比如 TreeSet 有序，HashSet 无序

TreeSet：基于红黑树实现，支持有序性操作，例如根据一个范围查找元素的操作。但是查找效率不如 HashSet，HashSet 查找的时间复杂度为 O(1)，TreeSet 则为 O(logN)。
HashSet：基于哈希表实现，支持快速查找，但不支持有序性操作。并且失去了元素的插入顺序信息，也就是说使用 Iterator 遍历 HashSet 得到的结果是不确定的。
LinkedHashSet：具有 HashSet 的查找效率，且内部使用双向链表维护元素的插入顺序。

List

ArrayList：基于动态数组实现，支持随机访问。
Vector：和 ArrayList 类似，但它是线程安全的。
LinkedList：基于双向链表实现，只能顺序访问，但是可以快速地在链表中间插入和删除元素。不仅如此，LinkedList 还可以用作栈、队列和双向队列。

Queue

队列，有序，严格遵守先进先出。

LinkedList：可以用它来实现双向队列。实现了 Queue 接口。
PriorityQueue：基于堆结构实现，可以用它来实现优先队列？？？内部是基于数组构建的，用法就是你自定义一个 comparator ，自己定义对比规则，这个队列就是按这个规则来排列出队的优先级。

2. Map

存储的是键值对，也就是给对象（value）搞了一个 key，这样通过 key 可以找到那个 value。

TreeMap：基于红黑树实现。有序。
HashMap：基于哈希表实现。
HashTable：和 HashMap 类似，但它是线程安全的，这意味着同一时刻多个线程可以同时写入 HashTable 并且不会导致数据不一致。它是遗留类，不应该去使用它。现在可以使用 ConcurrentHashMap 来支持线程安全，并且 ConcurrentHashMap 的效率会更高，因为 ConcurrentHashMap 引入了分段锁。
LinkedHashMap：使用双向链表来维护元素的顺序，顺序为插入顺序或者最近最少使用(LRU)顺序。

实现类

ArrayList

add(E e)     // 向列表末尾添加元素
get(int index)     // 获取指定索引位置的元素
size()     // 获取列表的大小
remove(int index)     // 移除指定索引位置的元素
contains(Object o)     // 判断是否包含指定元素

LinkedList

add(E e)     // 在列表末尾添加元素
addFirst(E e)   
addLast(E e)     // 在列表开头或末尾添加元素
get(int index)     // 获取指定索引位置的元素
remove(int index)    // 移除指定索引位置的元素
size()     // 获取列表的大小

Stack & Queue

1 2	push(E e) // 将元素压入栈顶 pop() // 移除栈顶元素

1 2	offer(E e) // 将元素添加到队列尾部 poll() // 获取并移除队列头部元素

PriorityQueue

1
2
3

add(E e)     //  向队列中添加元素
remove()     // 移除队列头部的元素
peek()     // 获取但不移除队列头部的元素

HashSet & HashMap

1
2
3

add(E e)     // 向集合中添加元素
contains(Object o)     // 判断集合是否包含指定元素
remove(Object o)     // 移除集合中指定的元素

put(K key, V value)     // 将键值对存入 Map
get(Object key)     // 获取指定键的值
containsKey(Object key)     // 判断 Map 是否包含指定键
remove(Object key)     // 移除 Map 中指定键的键值对

LinkedHashSet&Map

TreeSet & TreeMap

TreeSet
add(E e): 向集合中添加元素
contains(Object o): 判断集合是否包含指定元素
remove(Object o): 移除集合中指定的元素
TreeMap
put(K key, V value): 将键值对存入 Map
get(Object key): 获取指定键的值
containsKey(Object key): 判断 Map 是否包含指定键
remove(Object key): 移除 Map 中指定键的键值对

WeakHashMap

数据存储

在Java中，数据的存储方式涉及到内存的不同区域，主要包括堆内存和栈内存。

栈内存（Stack Memory）：
- 存储特点：栈内存用于存储局部变量（方法内部定义的变量）和方法调用的执行上下文（包括方法的参数、返回地址等信息）。每个线程都有自己的栈内存，用于管理方法调用和局部变量的生命周期。
- 生命周期：局部变量的生命周期与方法的执行周期相关联。当方法被调用时，会在栈内存中为局部变量分配内存，当方法执行完毕时，栈内存会自动释放局部变量的内存。
- 线程安全：栈内存是线程私有的，因此它是线程安全的。不同线程的栈内存互相独立，不会发生竞态条件。
堆内存（Heap Memory）：
- 存储特点：堆内存用于存储对象和数组等引用数据类型。是所有线程共享的内存区域，用于管理动态分配的对象的生命周期。
- 生命周期：对象在堆内存中的生命周期不受方法调用的限制。对象在被创建时分配内存，在不再被引用时会被垃圾回收器自动回收。
- 线程安全：由于堆内存是共享的，需要特别注意多线程访问的同步问题。Java提供了一些机制来确保堆内存中的数据安全，如 synchronized关键字和 java.util.concurrent 包中的工具类。
数据存储示例：
- 当创建一个对象时，对象的引用存储在栈内存中，而对象的实际数据存储在堆内存中。例如，Person person = new Person();
  1. 在堆内存中，会为Person对象分配内存空间，这个对象包含了Person类中定义的所有成员变量（属性）。例如，如果Person类有一个名为name的成员变量，那么堆内存中的Person对象将包含一个用于存储name属性值的内存位置。堆内存中的对象是独立的，每个new Person()创建一个新的对象，其数据在堆内存中不会重叠。
  2. 在栈内存中，会创建一个名为person的引用变量，这个引用变量存储了指向堆内存中Person对象的地址。也就是说，栈内存中的person变量实际上存储了对堆内存中Person对象的引用。当你访问person时，实际上是通过栈内存中的引用找到堆内存中的对象，然后可以操作对象的属性和方法。
- 局部变量（例如方法中的局部变量）的值和引用都存储在栈内存中。
- 数组的引用存储在栈内存中，而数组的元素（对象引用或基本数据类型）存储在堆内存中。
- 静态变量（static关键字修饰的变量）存储在方法区（在JVM规范中称为永久代）。

缓存池

Integer x = new Integer(123);
Integer y = new Integer(123);
System.out.println(x == y);    // false; new Integer() 每次都会新建一个对象
Integer z = Integer.valueOf(123);
Integer k = Integer.valueOf(123);
System.out.println(z == k);    // true; valueOf()会使用缓存池中的对象，多次调用会取得同一个对象的引用
Integer m = 123;
Integer n = 123;
System.out.println(m == n);    // true; 编译器会在缓冲池范围内的基本类型自动装箱过程调用 valueOf() 
// 因此多个 Integer 实例使用自动装箱来创建并且值相同，那么就会引用相同的对象。

运算

参数传递

在Java中，方法参数的传递方式是按值传递，而不是引用传递。这意味着当你将参数传递给方法时，实际上是将参数的值传递给了方法，而不是参数本身。这包括基本数据类型和对象引用。
1、基本数据类型： 作为参数传递的是该数据的副本。任何在方法内部对参数值的修改都不会影响到原始数据。
2、对象引用： 对象引用也是按值传递的，但需要理解的是对象引用指的是对象在内存中的地址（间接引用，非直接地址）。当你将一个对象作为参数传递给方法时，传递的是对象引用的副本，而不是对象本身。这意味着在方法内部可以修改对象的状态，但不能改变对象引用指向的内存地址。

隐式类型转换

“2.5” 字面量属于 double 类型，不能直接将 2.5 直接赋值给 float 变量，因为Java 不能隐式执行向下转型，这会使得精度降低。
1
float f = 2.5f; // 错误写法：float f = 2.5;
字面量 1 是 int 类型，它比 short 类型精度要高，因此不能隐式地下转型。但是使用 += 运算符可以执行隐式类型转换。
1
2
short s1 = 1; // 不能 s1 = s1 + 1;
s1 += 1; // 相当于 s1 = (short) (s1 + 1);

有/无符号数，原/反/补码

在 Java 中，所有的整数类型都是有符号的。Java中并没有内置的无符号整数类型；如果真的需要，可以使用大整数类 BigInteger。
无符号整数通常用于表示大范围正整数值，以及位运算和处理原始数据。它们可以扩展表示的范围，因为不需要一位来表示符号。
原码是最简单的表示形式，其中最高位表示符号（0正数，1负数），其余位表示数值的大小。例如，+3原码为0011，-3原码为1011。
反码是对原码的符号位以外的位取反得到的结果。正数的反码与其原码相同，负数的反码是其原码除符号位外取反。
补码是计算机中最常用的表示方式。补码的计算方法是对反码加1。正数的补码与其原码相同，负数的补码是其反码加1。
在Java中，整数类型（如byte、short、int、long）使用补码来表示有符号整数。这种表示方式使得负数的加法和减法运算可以与正数的运算使用同一套算法来执行，简化了计算机中的运算。

位运算

在 Java 中，位运算是操作二进制位的一种操作，它们可以用来执行诸如位移、与、或、非等操作。

int a = 5, b = 3;  // 二进制表示：0101, 0011
int andResult = a & b;  // 0101 & 0011 = 0001，结果为 1
int orResult = a | b;   // 0101 | 0011 = 0111，结果为 7
int xorResult = a ^ b;  // 0101 ^ 0011 = 0110，结果为 6
int complementA = ~a;   // ~0101 = 1010（补码表示），结果为 -6（-6的八位补码就是1111 1010）
int leftShift = a << 1;            // 0101 左移 1 位 = 1010，结果为 10
int rightShift = a >> 1;           // 0101 右移 1 位 = 0010，结果为 2（使用符号位填充空位）
int unsignedRightShift = a >>> 1;  // 0101 无符号右移 1 位 = 0010，结果为 2（使用 0 填充空位）

在 Java 中，十六进制表示使用前缀 0x 或者 0X 来标识一个十六进制数。
使用位运算符时：Java 内部会将这些十六进制数转换为对应的二进制形式，然后执行位运算操作，最后转换回十六进制的结果。

int hex1 = 0xA, hex2 = 0x7;          // 十六进制数 A 对应十进制数 10, 十六进制数 7 对应十进制数 7
int andResult = hex1 & hex2;         // 十六进制数 A & 7 = 1010 & 0111 = 0010，结果为 2
int complementHex1 = ~hex1;          // ~1010 = 0101（补码表示），结果为 -11
int rightShift = hex1 >> 1;          // 十六进制数 A 右移 1 位 = 1010 右移 1 位 = 0101，结果为 5
int unsignedRightShift = hex1 >>> 1; // A 无符号右移 1 位 = 1010 无符号右移 1 位 = 0101，结果为 5

n & (n−1)，把 n 的二进制位中的最低位的 1 变为 0。

颠倒给定的 32 位无符号整数 n 的二进制位

for(int i = 0; i < 32 && n != 0; i++) {
    ans = ans | (n & 1) << (31 - i);
    n >>>= 1;
}

类与对象

类（Class）： 类是对象的模板，它定义了对象的属性（成员变量）和行为（方法）。类是一种抽象的概念，描述了一类事物的共同特征。在Java中，类是一种引用数据类型。
对象（Object）： 对象是类的实例，是具体的、实际存在的数据。每个对象都有自己的状态（成员变量的值）和行为（方法的调用)

创建

创建对象实例： 使用关键字 new 可以创建一个类的对象。例如：
1
MyClass myObject = new MyClass();
通过反射： 使用 Java 的反射机制可以在运行时获取类的信息，创建对象实例。例如：
1
2
Class<?> clazz = Class.forName("com.example.MyClass");
MyClass myObject = (MyClass) clazz.newInstance();
通过工厂方法： 有时候，对象的创建可能通过工厂方法，例如静态方法等来实现。
通过new创建实例对象demo，放在堆内存上；然后再main方法的栈帧中存放一个局部变量，存放了demo对象在堆上的地址，即建立起一个引用关系。将局部变量置null后，引用就不存在了，堆上的实例对象demo就可以回收了。

使用

1
2
3

// 一旦对象被创建，可以通过其引用调用其属性和方法
myObject.setSomeProperty("value");
String propertyValue = myObject.getSomeProperty();

回收

对象的回收： Java虚拟机通过垃圾回收器（Garbage Collector）来自动回收不再被引用的对象。垃圾回收器会定期检查程序中的对象，识别哪些对象没有被任何引用指向，然后释放它们占用的内存。这个过程是自动的，开发者无需手动管理大部分对象的内存。
在某些情况下，可以通过手动设置对象引用为null来提示垃圾回收器回收对象。但这通常不是必要的，因为现代的垃圾回收器在大多数情况下能够很好地管理内存。
对象的生命周期从创建开始，直到没有任何引用指向它时结束。垃圾回收器负责在对象不再被引用时将其销毁。
类的回收： 在Java中，类的回收通常不是显式的操作。类加载和卸载是由类加载器（ClassLoader）来管理的。当一个类不再被任何对象引用，并且ClassLoader不再需要这个类时，该类可能会被卸载。在标准的Java应用程序中，类的卸载通常不是很常见，因为大多数类在整个应用程序的生命周期内都是可见的。
需要注意的是，类的卸载是Java虚拟机实现的一个可选特性，不是所有的Java虚拟机都支持类的卸载。类的卸载通常发生在特定的环境中，比如一些动态生成和卸载类的场景。
总体而言，Java虚拟机通过垃圾回收器自动管理对象的内存，而类的加载和卸载通常由类加载器来处理。这种自动化的内存管理减轻了开发者的负担，使得Java程序更容易编写和维护。

继承

访问权限

Java 中有三个访问权限修饰符: private、protected 以及 public。可以对类或类中的成员(字段以及方法)加上访问修饰符，如果不加访问修饰符，表示包级可见（default，介于private和protected之间）。
private：私有访问修饰符。被 private 修饰的成员（字段、方法、内部类等）仅对定义它们的类可见。这意味着这些成员只能在同一个类内部访问，对于类的外部（其他类）是不可见的。
protected：受保护的访问修饰符。被 protected 修饰的成员对于定义它们的类、同一包内的其他类以及子类可见。在不同包中的类无法访问受保护成员。
public：公共访问修饰符。被 public 修饰的成员对于所有类都是可见的，无论是同一包内还是不同包中的类，都可以访问 public 成员。

extend 与 implement

extend（扩展）：使用于类之间的关系。用于创建类的子类（子类继承父类）。子类可以继承父类的属性和方法。一个类只能extend一个类，即Java是单继承的，但是可以通过接口实现来弥补这一不足。
implement（实现）：使用于接口与类之间的关系。用于让类实现一个或多个接口，implement多个接口，实现多继承的效果。 类实现接口时，需要提供接口中定义的所有方法的具体实现。

抽象类与接口

抽象类和抽象方法都使用 abstract 关键字进行声明。抽象类一般会包含抽象方法，抽象方法一定位于抽象类中。
抽象类和普通类最大的区别是，抽象类不能被实例化，需要继承抽象类才能实例化其子类。
接口是抽象类的延伸，在 Java 8 之前，它可以看成是一个完全抽象的类，也就是说它不能有任何的方法实现。从 Java 8 开始，接口也可以拥有默认的方法实现，这是因为不支持默认方法的接口的维护成本太高了。在 Java 8 之前，如果一个接口想要添加新的方法，那么要修改所有实现了该接口的类。接口的成员(字段 + 方法)默认都是 public 的，并且不允许定义为 private 或者 protected。接口的字段默认都是 static 和 final 的。

super

访问父类的构造函数: 可以使用 super() 函数访问父类的构造函数，从而委托父类完成一些初始化的工作。
访问父类的成员: 如果子类重写了父类的中某个方法的实现，可以通过使用 super 关键字来引用父类的方法实现。

public class SuperExample {
    protected int x, y;
    public SuperExample(int x, int y) {                this.x = x;     this.y = y;     }
    public void func() {                  System.out.println("SuperExample.func()");       }
}
public class SuperExtendExample extends SuperExample {
    private int z;
    public SuperExtendExample(int x, int y, int z) {   super(x, y);    this.z = z;     }
    @Override
    public void func() {  super.func();  System.out.println("SuperExtendExample.func()"); }
}
SuperExample e = new SuperExtendExample(1, 2, 3);
e.func();  // 结果：SuperExample.func() SuperExtendExample.func()

重载与重写

重载(Overload)存在于同一个类中，指一个方法与已经存在的方法名称上相同，但是参数类型、个数、顺序至少有一个不同。应该注意的是，返回值不同，其它都相同不算是重载。
重写(Override)存在于继承体系中，指子类实现了一个与父类在方法声明上完全相同的一个方法。为了满足里式替换原则，重写有以下两个限制:子类方法的访问权限必须大于等于父类方法；子类方法的返回类型必须是父类方法返回类型或为其子类型。使用 @Override 注解，可以让编译器帮忙检查是否满足上面的两个限制条件。

常用方法

Java标准库包含多个类和函数，提供了许多基本的工具和功能，包括但不限于：
1、java.lang - 包含Java的基础类，例如String、Object、System等。这个包是默认导入的，不需要手动引入。
2、java.util - 提供集合框架、日期时间工具、随机数生成器等。
3、java.io - 包含用于进行输入和输出的类和接口，例如File、InputStream、OutputStream等。
4、java.net - 提供了网络相关的类，比如URL、URLConnection等。
5、java.math - 包含用于数学计算的类，例如BigInteger、BigDecimal等。
6、java.nio - 提供了新的I/O类，支持非阻塞I/O、内存映射文件等。
7、java.util.concurrent - 包含用于并发编程的实用工具和框架。
8、java.awt 和 javax.swing - 提供了GUI开发相关的类。
大部分情况下，这些库中的类和函数默认可用，无需手动引入。然而，有一些更特定或较为不常用的类可能需要显式地引入相应的包。

数据处理

// 1. 保存两位小数；import java.text.DecimalFormat;（text在标准库中，通常不需要手动引入）
double number = 123.45678;
DecimalFormat decimalFormat = new DecimalFormat("#.##"); // 创建 DecimalFormat 对象并指定格式
String formattedNumber = decimalFormat.format(number);   // 将浮点数格式化为指定格式的字符串
// 2. 比大小：方法 java.lang.Math 中；小 Math.min()
int i = Math.max(647, 582);
// 3. 随机数：生成范围介于 0（包括）和指定边界（不包括）之间的随机整数
Random random = new Random();                       // 创建 Random 对象
int randomNumber = random.nextInt();                // 生成整数范围在 int 类型的取值范围内
int randomInRange = random.nextInt(10 - 5 + 1) + 5; // 生成整数范围 5 - 10
double randomDouble = random.nextDouble();          // 生成范围在 [0, 1) 之间的随机小数
// 4. 二进制，十六进制
String binaryString = Integer.toBinaryString(10);      // 整数表示为二进制字符串：1010
String hexString = Integer.toHexString(20);            // 整数表示为十六进制字符串：14
int decimalNumber = Integer.parseInt(binaryString, 2); // 二进制字符串转整数：10
int decimalNumber = Integer.parseInt(hexString, 16);   // 十六进制字符串转整数：20

Object 通用方法

在Java中，Object是所有类的基类。它是Java类继承层次结构的根，因此每个Java类都直接或间接地继承自Object类。Object类位于java.lang包中，这意味着它不需要显式导入就可以在Java程序中使用。

java.lang包是java语言的核心，提供基础类，包括基本Object类、Class类、String类、基本类型的包装类、基本的数学类等。

Object类定义了一些基本的方法，这些方法可以被所有的Java对象继承和使用。其中一些重要的方法包括：

public final native Class<?> getClass()     // 返回对象的运行时类（`Class`对象）。
public native int hashCode()                // 返回对象的哈希码值。它通常与`equals`方法一起使用，以便在使用哈希表等数据结构时能够快速查找对象。
public boolean equals(Object obj)           // 用于比较两个对象是否相等。默认情况下，它比较的是对象的内存地址，但可以在子类中重写以实现自定义的相等性比较。
protected native Object clone() throws CloneNotSupportedException    // 用于创建对象的浅拷贝。需要注意的是，为了使对象可克隆，子类需要实现`Cloneable`接口并重写`clone`方法。
public String toString()                    // 返回对象的字符串表示。默认下，它返回一个由类名和对象的哈希码组成的字符串，但可以在子类中重写以提供更有意义的字符串表示。
public final native void notify()           // 用于多线程同步的方法。
public final native void wait(long timeout) throws InterruptedException   // 使线程等待直到被通知。
protected void finalize() throws Throwable {}     // 在对象被垃圾回收之前调用的方法。

equals()

equals() 与 == 对于基本类型，== 判断两个值是否相等，基本类型没有 equals() 方法。
对于引用类型，== 判断两个变量是否引用同一个对象，而 equals() 判断引用的对象是否等价。

Integer x = new Integer(1);
Integer y = new Integer(1);
System.out.println(x.equals(y)); // true
System.out.println(x == y);      // false

hashCode()

返回对象的哈希码。默认实现是基于对象的内存地址生成哈希码。
在实际应用中，一般需要在类中重写该方法，以便相等的对象具有相同的哈希码，以提高哈希表等集合的性能。

clone()

cloneable：clone() 是 Object 的 protected 方法而非 public，一个类不显式去重写，其它类就不能直接调用该类实例的 clone()。
浅拷贝：拷贝对象和原始对象的引用类型引用同一个对象。
深拷贝：拷贝对象和原始对象的引用类型引用不同对象。
clone() 的替代方案：使用 clone() 方法来拷贝一个对象即复杂又有风险，它会抛出异常，并且还需要类型转换。Effective Java 书上讲到，最好不要去使用 clone()，可以使用拷贝构造函数或者拷贝工厂来拷贝一个对象。

异常

Throwable 可以用来表示任何可以作为异常抛出的类，分为两种: Error 和 Exception。
其中 Error 用来表示 JVM 无法处理的错误，Exception 分为两种:
- 受检异常 : 需要用 try…catch… 语句捕获并进行处理，并且可以从异常中恢复；
- 非受检异常 : 是程序运行时错误，例如除 0 会引发 Arithmetic Exception，此时程序崩溃并且无法恢复

反射

Java反射是一种强大的编程技术，允许在运行时检查、探索和操作类、对象、字段、方法以及其他成员。反射使你可以动态地创建对象、调用方法、获取和设置字段值，以及执行其他与类和对象相关的操作。

每个类都有一个 Class 对象，包含与类有关的信息。当编译一个新类时会产生一个同名的.class文件，其内容保存着 Class 对象。
类加载相当于 Class 对象的加载。类在第一次使用时才动态加载到 JVM 中，可以使用 Class.forName("com.mysql.jdbc.Driver") 这种方式来控制类的加载，该方法会返回一个 Class 对象。
反射可以提供运行时的类信息，并且这个类可以在运行时才加载进来，甚至编译时期该类的 .class 不存在也可以加载进来。
Class 和 java.lang.reflect 一起对反射提供了支持，java.lang.reflect 类库主要包含了以下三个类:
- Field : 可以使用 get() 和 set() 方法读取和修改 Field 对象关联的字段；
- Method : 可以使用 invoke() 方法调用与 Method 对象关联的方法；
- Constructor : 可以用 Constructor 创建新的对象。

Class类：Java反射的核心类是java.lang.Class。每个类都有一个与之相关的Class对象，你可以使用这个Class对象来获取关于类的信息。

// 获取类的`Class`对象
Class<?> myClass = MyClass.class; // 通过类名
Class<?> myClass = obj.getClass();  // 通过对象
Class<?> myClass = Class.forName("com.example.MyClass"); // 通过类的全名
// 获取有关类的信息
String className = myClass.getName(); // 获取类名
String packageName = myClass.getPackage().getName(); // 获取包名
Class<?> superClass = myClass.getSuperclass(); // 获取父类
Class<?>[] interfaces = myClass.getInterfaces(); // 获取实现的接口
Field[] fields = myClass.getDeclaredFields(); // 获取所有字段
Method[] methods = myClass.getDeclaredMethods(); // 获取所有方法

实例化对象：通过反射，你可以动态地创建对象。例如：

Class<?> myClass = Class.forName("com.example.MyClass");
Object obj = myClass.newInstance(); // 创建对象，需要无参构造函数
// 使用反射来获取、设置对象的字段值
Field field = myClass.getDeclaredField("fieldName");
field.setAccessible(true); // 设置字段可访问
Object value = field.get(obj); // 获取字段值
field.set(obj, newValue); // 设置字段值
// 反射允许你调用对象的方法。例如：
Method method = myClass.getDeclaredMethod("methodName", param1Type, param2Type);
method.setAccessible(true); // 设置方法可访问
Object result = method.invoke(obj, arg1, arg2); // 调用方法

数组与泛型：通过反射，你可以创建数组、获取数组元素的类型信息，以及处理泛型信息。
代理：Java反射还可用于创建动态代理，这是一种强大的技术，允许你创建实现特定接口的代理类以在运行时拦截和处理方法调用。
限制：尽管反射提供了强大的能力，但也有一些限制和性能开销。使用时需要小心处理异常、性能、访问控制等方面的问题。

泛型

泛型是 Java 中的一个核心特性，有助于提高代码的可重用性和类型安全性。

泛型的主要目的是参数化类型，允许你在类、接口、方法中使用类型参数。

public class Box<T> {
    private T t;  // T stands for "Type"
    public void set(T t) { this.t = t; }
    public T get() { return t; }
}
public class ChildBox<T> extends Box<T> {
    // 子类继承父类的泛型类型参数
}

泛型通配符：Java中有通配符类型，允许你在不知道具体类型的情况下使用泛型。通配符包括?符号。
当你使用通配符作为方法参数时，可能需要捕获通配符以使用它。这可以通过在方法参数中使用?来实现。
1
2
3
public void processList(List<?> list) {
for (Object obj : list) { // 处理每个元素 }
}
泛型上下界：你可以使用通配符来定义类型的上下界。例如，<? extends Number>表示类型必须是Number或其子类。<? super Integer>表示类型必须是Integer或其父类。
类型擦除：Java泛型通过类型擦除来实现。这意味着在编译时，泛型类型信息会被擦除，而在运行时，Java虚拟机将使用原始类型。这可能会导致一些限制，例如无法创建泛型数组。

注解

Java 注解是附加在代码中的一些元信息，用于一些工具在编译、运行时进行解析和使用，起到说明、配置的功能。注解不会也不能影响代码的实际逻辑，仅仅起到辅助性的作用。https://pdai.tech/md/java/basic/java-basic-x-annotation.html
Spring框架中的注解 本质上是一种元数据，用于为应用程序的组件（例如类、方法、字段等）提供附加的信息，以指导Spring容器在应用程序运行时如何处理这些组件。这些注解告诉Spring容器如何创建、初始化、配置和管理这些组件，以及它们之间的关系。

Stream 流

在Java中，流（Stream）是用于处理集合数据的一种新的抽象。Java的流操作主要分为两种：中间操作和终端操作。流的处理操作通常应用于集合类（如List、Set、Map等）。
Java的流操作利用了函数式编程的思想，提供了一种更简洁、灵活、可读性更强的处理方式。通过合理使用中间操作和终端操作，可以实现丰富的数据处理功能。流操作也广泛应用于Java集合、文件IO、网络编程等场景。

中间操作：

中间操作主要用于对数据进行处理和转换，产生一个新的流。中间操作不会触发实际的处理，只是在流上进行各种操作。

常见的中间操作包括 filter（过滤）、map（映射）、distinct（去重）、sorted（排序）、limit（限制结果数量）等。

List<String> names = Arrays.asList("Alice", "Bob", "Charlie", "David", "Alice");

names.stream()
     .filter(name -> name.length() > 3)
     .distinct()
     .sorted()
     .map(String::toUpperCase)
     .forEach(System.out::println);

终端操作：

终端操作是流的最终处理步骤，触发流的遍历和数据处理。终端操作会返回一个非流的结果，例如集合、数组、某个值等。

常见的终端操作包括 collect（将流元素收集到集合中）、reduce（对元素进行归约操作）等。

List<String> names = Arrays.asList("Alice", "Bob", "Charlie", "David", "Alice");

List<String> filteredNames = names.stream()
                                  .filter(name -> name.length() > 3)
                                  .distinct()
                                  .sorted()
                                  .map(String::toUpperCase)
                                  .collect(Collectors.toList());

??Lambda 表达式

学习 http://doc.junbo.top/pages/viewpage.action?pageId=10798971
Lambda 表达式提供了一种简洁、清晰的语法，允许以更为函数式的方式编写代码。
Lambda 的引入使得代码变得更加简洁，尤其在使用函数式接口（只有一个抽象方法的接口）时，可以直接传递 Lambda 表达式，而不再需要传递匿名内部类的实例。Lambda 表达式在处理集合、并发编程、事件处理等场景中广泛应用，它是 Java 8 引入的一个重要特性，使得 Java 语言更好地支持函数式编程风格。

Lambda 表达式主要用于定义内联的、匿名的函数。它是一个函数式接口的实例，即只有一个抽象方法的接口。基本语法如下：

// `parameters` 指定了 Lambda 表达式的参数，`->` 是 Lambda 操作符，
// `expression` 或 `{ statements; }` 指定了 Lambda 表达式的主体。
(parameters) -> expression
(parameters) -> { statements; }
// 1. 一个简单的例子，计算两个数的和：
(int a, int b) -> a + b
// 2. 遍历列表并打印每个元素：
List<String> list = Arrays.asList("apple", "banana", "orange");
list.forEach(s -> System.out.println(s));
// 3. 使用 `Runnable` 接口创建一个线程：
new Thread(() -> System.out.println("Hello, Lambda!")).start();

Java 动态代理机制 ??

代理可以分为 “静态代理” 和 “动态代理”，动态代理又分为 “JDK动态代理” 和 “CGLIB动态代理” 实现。

静态代理
代理对象和实际对象都继承了同一个接口，在代理对象中指向的是实际对象的实例，这样对外暴露的是代理对象而真正调用的是实际对象。
优点：可以很好的保护实际对象的业务逻辑对外暴露，从而提高安全性。
缺点：不同的接口要有不同的代理类实现，会很冗余
JDK 动态代理
为了解决静态代理中，生成大量的代理类造成的冗余；JDK 动态代理只需要实现 InvocationHandler 接口，重写 invoke 方法便可以完成代理的实现，jdk的代理是利用反射生成代理类 Proxyxx.class 代理类字节码，并生成对象 jdk动态代理之所以只能代理接口是因为代理类本身已经extends了Proxy，而java是不允许多重继承的，但是允许实现多个接口。
优点：解决了静态代理中冗余的代理实现类问题。
缺点：JDK 动态代理是基于接口设计实现的，如果没有接口，会抛异常。
CGLIB 代理
由于 JDK 动态代理限制了只能基于接口设计，而对于没有接口的情况，JDK方式解决不了；CGLib 采用了非常底层的字节码技术，其原理是通过字节码技术为一个类创建子类，并在子类中采用方法拦截的技术拦截所有父类方法的调用，顺势织入横切逻辑，来完成动态代理的实现。实现方式实现 MethodInterceptor 接口，重写 intercept 方法，通过 Enhancer 类的回调方法来实现。但是CGLib在创建代理对象时所花费的时间却比JDK多得多，所以对于单例的对象，因为无需频繁创建对象，用CGLib合适，反之，使用JDK方式要更为合适一些。同时，由于CGLib由于是采用动态创建子类的方法，对于final方法，无法进行代理。
优点：没有接口也能实现动态代理，而且采用字节码增强技术，性能也不错。
缺点：技术实现相对难理解些。

BIO、NIO 和 AIO 的区别

Java 设计模式

设计模式是为了解决软件开发过程中常见的问题而提出的一种解决方案，它们是从实际应用中总结出来的一些经验和方法论。设计模式可以帮助开发人员更加容易地解决复杂问题，提高代码的可重用性、可扩展性、可维护性等，从而提高软件开发效率和代码质量。
具体来说，设计模式主要是为了解决以下几类问题：
（1）代码复杂度问题：在软件开发中，代码往往会变得越来越复杂，难以理解和维护。设计模式提供了一些组织代码的方式，让代码结构更加清晰，易于理解和维护。
（2）重用问题：在开发过程中，我们希望能够尽可能地复用代码，减少重复开发的工作量。设计模式提供了一些通用的解决方案，可以让我们更加容易地复用代码。
（3）扩展性问题：软件开发过程中，我们需要不断地对系统进行扩展和改进。设计模式提供了一些可扩展的解决方案，可以让系统更加容易地扩展和改进，同时保持代码的高可读性和可维护性。
（4）协作问题：在多人协作的开发过程中，代码的组织和沟通变得非常重要。设计模式提供了一些标准化的组织方式，可以让开发者更加容易地沟通和协作。
设计原则
软件设计原则是指在软件开发过程中遵循的一些通用的、经过验证的规则和指导原则。这些原则旨在提高软件的可维护性、可扩展性、可重用性和可靠性等方面的质量。
以下是一些常见的软件设计原则：
（1）单一职责原则（SRP）：一个类应该只有一个职责或只有一个引起变化的原因。
（2）开放-封闭原则（OCP）：软件实体（类、模块、函数等）应该是可扩展的，但是不可修改的。
（3）里氏替换原则（LSP）：任何基类可以出现的地方，子类一定可以出现，而且不会导致任何错误或异常。
（4）依赖倒置原则（DIP）：高层模块不应该依赖于底层模块，二者都应该依赖于抽象。抽象不应该依赖于具体实现，具体实现应该依赖于抽象。
（5）接口隔离原则（ISP）：客户端不应该依赖于它不需要的接口。一个类对另一个类的依赖应该建立在最小的接口上。
（6）迪米特法则（LoD）：一个对象应该对其他对象有最少的了解。通俗地讲，就是一个类对自己依赖的类知道得越少越好。
（7）合成复用原则（CRP）：尽量使用对象组合，而不是继承来达到复用的目的。
高内聚，低耦合
高内聚低耦合是软件设计中的一个原则，它强调模块内部的联系应该紧密而模块之间的联系应该尽量松散。具体来说，高内聚指的是一个模块内部的各个组成部分之间的联系应该紧密，组成部分之间的关系应该尽量简单。低耦合指的是一个模块与其他模块之间的依赖关系应该尽量松散，即模块之间的耦合度应该尽量低。
高内聚的好处在于，一个模块内部的联系紧密，表示这个模块是一个独立的整体，对外部的干扰最小。同时，当需要对一个模块进行修改时，只需要修改该模块内部的某些部分，不会对其他部分造成影响，从而提高了系统的可维护性和可扩展性。
低耦合的好处在于，模块之间的联系松散，意味着这些模块之间的依赖性较小，当一个模块需要进行修改时，不会对其他模块产生影响，从而提高了系统的可维护性和可扩展性。
23种设计模式
- 创造型模式
  - 单例模式：确保一个类只有一个实例，并提供该实例的全局访问点
  - 工厂方法模式：它定义了一个创建对象的接口，但由子类决定要实例化哪个类。工厂方法把实例化操作推迟到子类
  - 抽象工厂模式：创建的是对象家族，也就是很多对象而不是一个对象，并且这些对象是相关的，也就是说必须一起创建出来。而工厂方法模式只是用于创建一个对象，这和抽象工厂模式有很大不同
  - 建造者模式：生成器(Builder)？模式，封装一个对象的构造过程，并允许按步骤构造
  - 原型模式：使用原型实例指定要创建对象的类型，通过复制这个原型来创建新对象
- 结构型模式
  - 适配器模式：将一个类的接口, 转换成客户期望的另一个接口。适配器让原本接口不兼容的类可以合作无间。对象适配器使用组合, 类适配器使用多重继承
  - 代理模式：为另一个对象提供一个替身或占位符以控制对这个对象的访问
  - 桥接模式：使用桥接模式通过将实现和抽象放在两个不同的类层次中而使它们可以独立改变
  - 装饰器模式：动态地将责任附加到对象上, 若要扩展功能, 装饰者提供了比继承更有弹性的替代方案
  - 外观模式：它提供了一个统一的接口，用来访问子系统中的一群接口，从而让子系统更容易使用
  - 组合模式：允许你将对象组合成树形结构来表现”整体/部分”层次结构. 组合能让客户以一致的方式处理个别对象以及对象组合
  - 享元模式：利用共享的方式来支持大量细粒度的对象，这些对象一部分内部状态是相同的。它让某个类的一个实例能用来提供许多”虚拟实例”
- 行为型模式
  - 观察者模式：在对象之间定义一对多的依赖, 这样一来, 当一个对象改变状态, 依赖它的对象都会收到通知, 并自动更新
  - 策略模式：定义了算法族, 分别封闭起来, 让它们之间可以互相替换, 此模式让算法的变化独立于使用算法的客户
  - 命令模式：将”请求”封闭成对象, 以便使用不同的请求,队列或者日志来参数化其他对象. 命令模式也支持可撤销的操作
  - 中介者模式：使用中介者模式来集中相关对象之间复杂的沟通和控制方式
  - 备忘录模式：当你需要让对象返回之前的状态时(例如, 你的用户请求”撤销”), 你使用备忘录模式
  - 模版方式模式：在一个方法中定义一个算法的骨架, 而将一些步骤延迟到子类中. 模板方法使得子类可以在不改变算法结构的情况下, 重新定义算法中的某些步骤
  - 迭代器模式：提供一种方法顺序访问一个聚合对象中的各个元素, 而又不暴露其内部的表示
  - 状态模式：允许对象在内部状态改变时改变它的行为, 对象看起来好象改了它的类
  - 责任链模式：通过责任链模式, 你可以为某个请求创建一个对象链. 每个对象依序检查此请求并对其进行处理或者将它传给链中的下一个对象
  - 解释器模式：使用解释器模式为语言创建解释器，通常由语言的语法和语法分析来定义
  - 访问者模式：当你想要为一个对象的组合增加新的能力, 且封装并不重要时, 就使用访问者模式

单例模式

什么是单例设计模式？
单例模式是⼀种创建型设计模式，它的核⼼思想是保证⼀个类只有⼀个实例，并提供⼀个全局访问点来访问这个实例。
只有⼀个实例的意思是，在整个应⽤程序中，只存在该类的⼀个实例对象，⽽不是创建多个相同类型的对象。
全局访问点的意思是，为了让其他类能够获取到这个唯⼀实例，该类提供了⼀个全局访问点（通常是⼀个静态⽅法），通过这个⽅法就能获得实例。
为什么要使⽤单例设计模式呢？
1. 全局控制：保证只有⼀个实例，这样就可以严格的控制客户怎样访问它以及何时访问它，简单的说就是对唯⼀实例的受控访问（引⽤⾃《⼤话设计模式》第21章）
2. 节省资源：也正是因为只有⼀个实例存在，就避免多次创建了相同的对象，从⽽节省了系统资源，⽽且多个模块还可以通过单例实例共享数据。
3. 懒加载：单例模式可以实现懒加载，只有在需要时才进⾏实例化，这⽆疑会提⾼程序的性能。
单例设计模式的基本要求
1. 私有的构造函数：防⽌外部代码直接创建类的实例
2. 私有的静态实例变量：保存该类的唯⼀实例
3. 公有的静态⽅法：通过公有的静态⽅法来获取类的实例
单例模式的实现⽅式有多种，包括懒汉式、饿汉式等。
饿汉式指的是在类加载时就已经完成了实例的创建，不管后⾯创建的实例有没有使⽤，先创建再说，所以叫做“饿汉”。
懒汉式指的是只有在请求实例时才会创建，如果在⾸次请求时还没有创建，就创建⼀个新的实例，如果已经创建，就返回已有的实例，意思就是需要使⽤了再创建，所以称为“懒汉”

饿汉模式（线程安全）：类⼀加载就创建对象，这种⽅式⽐较常⽤。

优点：线程安全，没有加锁，执⾏效率较⾼。
缺点：不是懒加载，类加载时就初始化，浪费内存空间。
如何保证线程安全：基于类加载机制避免了多线程的同步问题，但是如果类被不同的类加载器加载就会创建不同的实例。

public class Singleton  {
    // 1、私有化构造⽅法，防⽌外部实例化
    private Singleton(){}
    // 2、定义⼀个静态变量指向⾃⼰类型
    private final static Singleton instance = new Singleton();
    // 3、对外提供⼀个公共的⽅法获取实例
    public static Singleton getInstance() {
        return instance;
    }
}

懒汉模式（线程安全）

懒汉模式在单线程下使⽤没有问题，对于多线程是⽆法保证单例的。
通过 synchronized 关键字加锁保证线程安全，synchronized 可以添加在⽅法上⾯，也可以添加在代码块上⾯，这⾥演示添加在⽅法上⾯，存在的问题是每⼀次调⽤ getInstance 获取实例时都需要加锁和释放锁，这样是⾮常影响性能的。
优点：懒加载，线程安全。
缺点：效率较低。

public class Singleton  {
    // 1、私有化构造⽅法
    private Singleton(){ }
    // 2、定义⼀个静态变量指向⾃⼰类型
    private static Singleton instance;
    // 3、对外提供⼀个公共的⽅法获取实例
    public synchronized static Singleton getInstance() {
        if (instance == null) {
            instance = new Singleton();
        }
        return instance;
    }
}

什么时候使⽤单例设计模式？

说了这么多，那在什么场景下应该考虑使⽤单例设计模式呢？可以结合单例设计模式的优点来看。

资源共享
多个模块共享某个资源的时候，可以使⽤单例模式，⽐如说应⽤程序需要⼀个全局的配置管理器来存储和管理配置信息、亦或是使⽤单例模式管理数据库连接池。
只有⼀个实例
当系统中某个类只需要⼀个实例来协调⾏为的时候，可以考虑使⽤单例模式，⽐如说管理应⽤程序中的缓存，确保只有⼀个缓存实例，避免重复的缓存创建和管理，或者使⽤单例模式来创建和管理线程池。
懒加载
如果对象创建本身就⽐较消耗资源，⽽且可能在整个程序中都不⼀定会使⽤，可以使⽤单例模式实现懒加载。
在许多流⾏的⼯具和库中，也都使⽤到了单例设计模式，⽐如Java中的 Runtime 类就是⼀个经典的单例，表示程序的运⾏时环境。此外 Spring 框架中的应⽤上下⽂ ( ApplicationContext ) 也被设计为单例，以提供对应⽤程序中所有 bean 的集中式访问点

工厂方法模式

什么是⼯⼚⽅法模式？
⼯⼚⽅法模式也是⼀种创建型设计模式，简单⼯⼚模式只有⼀个⼯⼚类，负责创建所有产品，如果要添加新的产品，通常需要修改⼯⼚类的代码。
⽽⼯⼚⽅法模式引⼊了抽象⼯⼚和具体⼯⼚的概念，每个具体⼯⼚只负责创建⼀个具体产品，添加新的产品只需要添加新的⼯⼚类⽽⽆需修改原来的代码，这样就使得产品的⽣产更加灵活，⽀持扩展，符合开闭原则。
⼯⼚⽅法模式分为以下⼏个⻆⾊：
抽象⼯⼚：⼀个接⼝，包含⼀个抽象的⼯⼚⽅法（⽤于创建产品对象）。
具体⼯⼚：实现抽象⼯⼚接⼝，创建具体的产品。
抽象产品：定义产品的接⼝。
具体产品：实现抽象产品接⼝，是⼯⼚创建的对象。
应⽤场景
⼯⼚⽅法模式使得每个⼯⼚类的职责单⼀，每个⼯⼚只负责创建⼀种产品，当创建对象涉及⼀系列复杂的初始化逻辑，⽽这些逻辑在不同的⼦类中可能有所不同时，可以使⽤⼯⼚⽅法模式将这些初始化逻辑封装在⼦类的⼯⼚中。在现有的⼯具、库中，⼯⼚⽅法模式也有⼴泛的应⽤，⽐如：
Spring 框架中的 Bean ⼯⼚：通过配置⽂件或注解，Spring 可以根据配置信息动态地创建和管理对象。
JDBC 中的 Connection ⼯⼚：在 Java 数据库连接中， DriverManager 使⽤⼯⼚⽅法模式来创建数据库连接。不同的数据库驱动（如 MySQL、PostgreSQL 等）都有对应的⼯⼚来创建连接

配适器模式

概念：适配器模式就是将⼀个类的接⼝，转换成客户期望的另⼀个接⼝。
作用：可以让原本两个不兼容的接⼝能够⽆缝完成对接。
原理 or 实现：适配器实现了其中一个对象的接口，并对另一个对象进行封装。

Java 各版本的新特性

New highlights in Java SE 8
Lambda Expressions，Pipelines and Streams，Date and Time API，Default Methods，Type Annotations，Nashhorn JavaScript Engine，Concurrent Accumulators，Parallel operations，PermGen Error Removed
New highlights in Java SE 7
Strings in Switch Statement，Type Inference for Generic Instance Creation，Multiple Exception Handling，Support for Dynamic Languages，Try with Resources，Java nio Package，Binary Literals,Underscore in literals，Diamond Syntax

Java 与 C++ 的区别

Java 是纯粹的面向对象语言，所有的对象都继承自 java.lang.Object，C++ 为了兼容 C 即支持面向对象也支持面向过程。
Java 通过虚拟机从而实现跨平台特性，但是 C++ 依赖于特定的平台。
Java 没有指针，它的引用可以理解为安全指针，而 C++ 具有和 C 一样的指针。
Java 支持自动垃圾回收，而 C++ 需要手动回收。
Java 不支持多重继承，只能通过实现多个接口来达到相同目的，而 C++ 支持多重继承。
Java 不支持操作符重载，而 C++ 可以。虽然可以对两个 String 对象支持加法运算，但是这是语言内置支持的操作，非操作符重载
Java 的 goto 是保留字，但是不可用，C++ 可以使用 goto。
Java 不支持条件编译，C++ 通过 #ifdef #ifndef 等预处理命令从而实现条件编译。

知识体系

Java全栈知识体系：https://pdai.tech/

2021-08-31

java 后端开发工程师

技术架构

Spring Boot：Java 生态首选框架之一，基于且进一步简化了Spring。
Spring：轻量级框架，用于构建企业级 Java 应用程序。
Spring MVC：处理浏览器请求，三层架构， MVC模式三层集体解决表现层的问题
MyBatis：处理访问数据库
Redis【6379】操作内存的数据库，Kafka【9092】消息队列服务器，Elasticsearch【9200】搜索引擎
Spring Cloud：微服务，project，module？？

开发环境

构建工具：Apache Maven
集成开发工具：IntelliJ IDEA
数据库：MySQL、Redis
应用服务器：Apache Tomcat【8080】（Spring Boot 默认以jar包集成了 Tomcat 作为内嵌的 Servlet 容器）
版本控制工具：Git
运维工具：Kubernetes 容器编排平台，FinalShell连接linux服务器

Java

常用 Java8 即 jdk1.8，安装jdk-8u202-windows-x64，配环境：把主目录配到 JAVA_HOME，bin 目录配到 PATH
安装配置好jdk，maven，git，idea后，基本可以开始开发

Apache Maven

Maven 帮助我们构建项目、管理项目中的jar包；系统环境：安装路径配到 MAVEN_HOME，bin 目录配到 PATH
本地仓库默认位置 ~/.m2/repository，存放从远程仓库获取的 jar 包；本机上的Maven主路径 D:/apache-maven-3.6.1，对应的用户配置文件为 D:\apache-maven-3.6.1\conf\settings.xml（更换为公司的maven配置文件）
在 https://mavenrepository.com 查找需要的jar包。配置阿里云镜像仓库 https://maven.aliyun.com/repository/central
中央仓库：是 Maven 的默认仓库，包含了大量的开源 Java 类库、框架和插件，许多常用的第三方库，供开发者使用。
镜像仓库：中央仓库的镜像，如阿里云、华为云，从中央仓库同步数据，用来加速依赖的下载速度，减轻中央仓库的负担。
私服仓库：在本地或者组织内部搭建的仓库，用于存储内部开发所需的依赖和构建产物。
在 IntelliJ IDEA 中配置 maven仓库：”File” > “Settings” > “Build, Execution, Deployment” > “Build Tools” > “Maven”，配置maven主路径、用户设置文件和本地仓库。

Maven 是一个强大的构建工具，它可以执行各种命令来管理项目的构建、依赖、测试等方面的任务。
以下是一些常用的Maven指令，进入项目根目录命令行终端执行：(当然也可以直接在idea点击按钮执行)

mvn clean            # 清除项目的目标目录，删除编译生成的文件。
mvn compile          # 编译项目中的Java源代码文件，并将编译结果放置在项目的目标目录(通常是target目录)中
mvn test             # 运行项目的单元测试。
mvn package          # 将项目打包为可执行的JAR或WAR文件，通常用于构建最终的可部署应用程序。
mvn install          # 将项目构建输出的JAR或WAR文件安装到本地Maven仓库，以便其他项目可以引用它作为依赖。
mvn deploy           # 将项目构建输出的JAR或WAR文件部署到远程仓库，通常用于共享依赖。
mvn clean install    # 用于先清除项目目录，然后执行安装操作。（引入pom中新加的dependence）
mvn clean package    # 用于先清除项目目录，然后执行打包操作。

JAR（Java Archive）是Java平台中用于打包和分发Java类和相关资源的文件格式。它是一种压缩格式，通常包含Java类文件（.class文件），资源文件，清单文件（Manifest），以及其他可以用于Java应用程序的元数据。
WAR（Web Application Archive）文件是一种Java Web应用程序的打包格式，通常用于部署Web应用程序到Java EE应用服务器，如Tomcat、WebSphere、或JBoss等。是一种压缩文件，通常以.war扩展名结尾，它包含了用于部署和运行Web应用程序的各种资源。

Gradle

Java作为一门世界级主流编程语言，有一款高效易用的项目管理工具是java开发者共同追求的心原和目标。
2012年基于 Ant 和Maven产生的Gradle，弥补了不足，带来了一些更高效的特点。它使用种基于Groovy的特定领域语言(DSL)来声明项目设置，抛弃了基于XML的各种繁琐配置。面向Java应用为主。
系统环境：安装路径配到 GRADLE_HOME，bin 目录配到 PATH
集成 IDEA：创建项目时，”Build System” 直接使用 Gradle 插件即可，选择本地安装的 Gradle 目录。
Gradle 目录结构与 Maven 完全一样：src/main/java 放置正式代码目录，src/main/resources 放置正式配置文件，src/test/java 放置单元测试代码，src/test/resources 放置测试配置文件，src/main/webapp 放置页面元素。
借助 spring 脚手架创建 Gradle 项目：https://start.spring.io/

Gradle 配置文件 build.gradle，使用 Groovy 编写（一种脚本语言）

// Gradle会首先搜索本地仓库（默认C:\Users\admin\.gradle）以查找依赖项
repositories {
    mavenLocal()
    // 如果未在本地仓库找到，Gradle将会去 mavenCentral() 仓库中查找
    mavenCentral()
}
// gradle工程所有的jar包在 dependencies 属性中，每一个jar包坐标有三个元素组成：group、name、version
// testCompile 表示该 jar包在测试的时候起作用，该属性为包的作用域
dependencies {
    testImplementation 'org.junit.jupiter:junit-jupiter-api:5.8.1'
    testRuntimeOnly 'org.junit.jupiter:junit-jupiter-engine:5.8.1'
    // 到 https://mvnrepository.com/ 查到 Spring Context 的 Gradle 依赖
    implementation group: 'org.springframework', name: 'spring-context', version: '5.0.2.RELEASE'
}

也可以直接把 Gradle 本地仓库配置成 Mavne 本地仓库，合二为一。具体做法是新建环境变量 GRADLE_USER_HOME 为 Mavne本地仓库目录，这样 Gradle工程会从 Mavne本地仓库目录寻找 jar包。

Spring Boot

核心作用：起步依赖、自动配置、端点监控
在 https://start.spring.io 创建一个springboot项目
Spring（Spring Framework）是一个开源的轻量级Java企业应用程序开发框架，旨在简化Java应用程序的开发。Spring本身并不直接管理Maven依赖，而是依赖Maven作为构建工具来管理项目中的依赖关系
Spring Boot 是 Spring 框架的一个扩展，旨在简化 Spring 应用程序的开发和部署。引入了 Starter 依赖的概念，这些 Starter是预配置的依赖项集合，用于快速启动特定类型的应用程序（例如，spring-boot-starter-web 是用于构建 Web 应用程序的 Starter 依赖，它包含了 Spring MVC、Tomcat 等依赖）;可以根据项目需求选择性地引入 Starter 依赖，而不必手动添加一堆依赖项。
1
2
3
4
<dependency> // 在 pom.xml 中配置需要的各种 spring-boot-starter 包
<groupId>org.springframework.boot</groupId>
<artifactId>spring-boot-starter-aop</artifactId>
</dependency>

Spring

Spring全家桶：Spring Framework, Spring Boot, Spring Cloud 微服务, Spring Cloud Data Flow 客户端
Spring Framework：
Spring Core - IoC, AOP 管理一切
Spring Data Access - Transactions, Spring MyBatis
Web Servlet - Spring MVC
Integration - Email, Scheduling, AMQP, Security
for more -> https://leo710aka.github.io/2021/09/11/Spring/

Spring MVC

三层架构：表现层、业务层、数据访问层
MVC：解决表现层的问题（Model：模型层 - View：视图层 - Controller：控制层）
HTTP：用于传输HTML等内容的应用层协议，规定了浏览器和服务器(或本地tomcat)之间如何通信以及通信时的数据格式。
核心组件 - 前端控制器：DispatcherServlet，控制整个MVC
Thymeleaf（View层）：模板文件 + Model -> 模板引擎（Thymeleaf） -> Html （但现在更多是前后端分离，会使用HTML+AJAX(异步请求)，采用前端框架进行渲染会更好的解耦）
在controller中写一个函数，获取数据，用model封装返回给html，在html文件中链接Thymeleaf模板，将数据动态展现。

Mysql

社区版下载zip文件：https://dev.mysql.com/downloads/mysql/
mysql及navicat配置：https://blog.csdn.net/taiyang3285/article/details/130115829
注意管理员运行cmd，然后把bin配到PATH、配置本机 username: root，password: “0xxxxx”

在application.properties文件配置 java(spring)项目连接 mysql，然后通过 Mybatis这样的持久层框架对数据库操作

spring:
  datasource:
    druid:
      driver-class-name: com.mysql.cj.jdbc.Driver
      url: jdbc:mysql://localhost:3306/reggie?serverTimezone=Asia/Shanghai&useUnicode=true&characterEncoding=utf-8&zeroDateTimeBehavior=convertToNull&useSSL=false&allowPublicKeyRetrieval=true
      username: root
      password: "078114"
mybatis-plus: ...

Mybatis

在pom.xml中导包后，在application.properties文件配置 mybatis
SqlSessionFactory: 用于创建SqlSession的工厂类。
SqlSession：MyBatis的核心组件，用于向数据库执行SQL。
主配置文件：XML配置文件，可以对MyBatis的底层行为做出详细的配置
Mapper接口：就是DAO接口，在MyBatis中习惯性的称之为Mapper。
Mapper映射器: 用于编写SQL，并将SQL和实体类映射的组件。采用XML、注解均可实现。
方法1：在 /java/../dao 下创建xxMapper.java（mapper接口）后，在 /resource/mapper 下创建对应的 xx-mapper.xml（映射器）；
方法2：直接在mapper中加@Select等注解里写sql（复杂sql还得方法1）

Mybatis-Plus

是在MyBatis基础上的扩展。只做增强不做改变，为简化开发、提高效率而生。
MyBatisPlus官方提供了starter，其中集成了 Mybatis和 MybatisPlus的所有功能，并且实现了自动装配效果。因此可以用 MybatisPlus的starter直接代替 Mybatis的starter；
1
2
3
4
5
<dependency>
<groupId>com.baomidou</groupId>
<artifactId>mybatis-plus-boot-starter</artifactId>
<version>3.5.3.1</version>
</dependency>

Redis

Redis是一款基于键值对的 NoSQL 数据库，它的值支持多种数据结构：字符串(strings)、哈希(hashes)、列表(lists)、集合(sets)、有序集合(sorted sets)等。 Redis将所有的数据都存放在内存中，所以它的读写性能十分惊人。同时，Redis还可以将内存中的数据以快照或日的形式保存到硬盘上，以保证数据的安全性。
Redis典型的应用场景包括: 缓存、排行榜、计器、社交网络、消息队列等.

Spring整合Redis：

引入依赖：在pom.xml中导包spring-boot-starter-data-redis
配置数据库参数：propert中 spring.redis.database=11 spring.redis.host=localhost spring.redis.port=6379

编写配置类，构造RedisTemplate（spring本身对redis的配置使其key为object类型，但string用起来更方便

@Configuration
public class RedisConfig {
    @Bean
    public RedisTemplate<String, Object> redisTemplate(RedisConnectionFactory factory) {
        RedisTemplate<String, Object> template = new RedisTemplate<>();
        template.setConnectionFactory(factory);                  
        template.setKeySerializer(RedisSerializer.string());     // 设置key的序列化方式
        template.setValueSerializer(RedisSerializer.json());     // 设置value的序列化方式
        template.setHashKeySerializer(RedisSerializer.string()); // 设置hash的key的序列化方式
        template.setHashValueSerializer(RedisSerializer.json()); // 设置hash的value的序列化方式
        template.afterPropertiesSet();
        return template;      }  }

访问Redis：redisTemplate.opsForValue()， redisTemplate.opsForHash， redisTemplate.opsForList()，redisTemplate.opsForSet()，redisTemplate.opsForZSet()

for more -> https://leo710aka.github.io/2022/03/12/Redis/

Kafka

阻塞队列（消息系统的底层）:
- BlockingQueue：处理并发和线程间的通信，帮助避免竞态条件、死锁等问题，并提高了系统的可维护性和性能。主要用于多线程编程中，以协调多个线程之间的数据传递、任务调度和同步操作。阻塞方法: put、take。
- 生产者消费者模式 - 生产者:产生数据的线程 - 消费者:使用数据的线程。
- 实现类 - ArrayBlockingQueue - LinkedBlockingQueue - PriorityBlockingQueue、SSynchronousQueue、DelayQueue等
Kafka是一个分布式的流媒体平台应用
- 应用：消息系统（消息队列）、日志收集、用户行为追踪、流式处理
- 特点：高吞吐量、消息持久化（硬盘）、高可靠性（顺序读写）、高扩展性（集群部署）
- 术语：- Broker（服务器）、Zookeeper - Topic（存放空间）、Partition（分区）、Offset（索引）
  Leader Replica（主副本）、Follower Replica

启动服务

配置：在 \config\zookeeper.properties 配置数据存放位置 dataDir=d:/work/data/zookeeper，在 server.properties 配置日志存放位置 log.dirs=d:/work/data/kafka-logs

命令行启动

# 在根目录 D:\kafka_2.12-2.3.0 打开cmd【1】，启动Apache Kafka的ZooKeeper服务器
D:\kafka_2.12-2.3.0>bin\windows\zookeeper-server-start.bat config\zookeeper.properties
# 在根目录 再打开一个cmd【2】，启动Kafka服务器 
D:\kafka_2.12-2.3.0>bin\windows\kafka-server-start.bat config\server.properties
# 在命令目录 D:\kafka_2.12-2.3.0\bin\windows 打开一个cmd【3】
# 创建topic，partition，replication，，， 开启 生产者
D:\kafka_2.12-2.3.0\bin\windows>kafka-topics.bat --create --bootstrap-server localhost:9092 --replication-factor 1 --partitions 1 --topic test
D:\kafka_2.12-2.3.0\bin\windows>kafka-console-producer.bat --broker-list localhost:9092 --topic test
# 在命令目录 再打开一个cmd【4】，， 开启 消费者
D:\kafka_2.12-2.3.0\bin\windows>kafka-console-consumer.bat --bootstrap-server localhost:9092 --topic test --from-beginning

Spring整合Kafka

引入依赖: spring-kafka
配置Kafka: spring.kafka.bootstrap-servers=localhost:9092，spring.kafka.consumer.group-id=community-consumer-group，spring.kafka.consumer.enable-auto-commit=true，spring.kafka.consumer.auto-commit-interval=3000

通过KafkaTemplate进行操作：

// 生产者（主动调用）
@Autowired
private KafkaTemplate kafkaTemplate;
kafkaTemplate.send(topic， data);
// 消费者（被动调用）
@KafkaListener(topics = {"test"})
public void handleMessage(ConsumerRecord record) {}

Kafka使用
把kafka发送系统通知的行为当做“事件”，操作不同topic就是处理不同种类的事件。
- 触发事件：评论后发布通知，点赞后发布通知，关注后发布通知
- 处理事件：封装事件对象（entity），开发事件的生产者，开发事件的消费者
- 在需要使用消息队列的controller中调用生产者（评论后发通知，点赞后发通知，关注后发通知），消费者（用户收到系统通知）将被动调用；一个消费者可以消费多种事件

Elasticsearch

Elasticsearch简介 （Es可以看成是一个特殊的数据库，是在这个“数据库”中进行搜索）
- 一个分布式的、Restful风格的搜索引擎。支持对各种类型的数据的检索
- 搜索速度快，可以提供实时的搜索服务
- 便于水平扩展，每秒可以处理PB级海量数据
Elasticsearch术语
- 索引、类型、文档、字段。（相当于MySQL中的数据库、表、行、列）（6.0后类型被废弃，则索引直接对应mysql的表）
- 集群（分布式集群部署）、节点（集群中的一台服务器）、分片（进一步划分索引并发存储）、副本（对分片备份）。
配置：目录D:\elasticsearch-6.4.3\config，文件elasticsearch.yml，修改 cluster.name: nowcoder、path.data: D:\work\data\elasticsearch-6.4.3\data、path.logs: D:\work\data\elasticsearch-6.4.3\logs；把bin目录配到环境变量
- 中文分词插件 elasticsearch-analysis-ik，解压到 D:\elasticsearch-6.4.3\plugin\ik

启动：（windows系统）双击 D:\elasticsearch-6.4.3\bin 下的 elasticsearch.bat 批处理文件即可。

命令行操作（另开一个cmd）

C:\Users\蔡枫>curl -X GET "localhost:9200/_cat/health?v"    # 查看集群的健康状态
C:\Users\蔡枫>curl -X GET "localhost:9200/_cat/nodes?v"     # 查看节点
C:\Users\蔡枫>curl -X GET "localhost:9200/_cat/indices?v"   # 查看索引
C:\Users\蔡枫>curl -X GET "localhost:9200/_cat/indices?v"
C:\Users\蔡枫>curl -X PUT "localhost:9200/test"             # 以put创建索引
{"acknowledged":true,"shards_acknowledged":true,"index":"test"}
C:\Users\蔡枫>curl -X DELETE "localhost:9200/test"          # 用http协议中的delete，删除索引
{"acknowledged":true}

Postman 操作
- GET，发送指令 localhost:9200/test/_doc/1 的request，查询test中的数据
- PUT，发送指令 localhost:9200/test/_doc/2 的request，向test中存数据，可以在Body中携带raw类型的json数据
- 搜索，GET，发送指令 localhost:9200/test/_search?q=xx:yy，搜索test索引下xx中带有yy的数据
- 复杂搜索：要在Body中带raw的json查询条件

Spring 整合 Es

引入依赖: spring-boot-starter-data-elasticsearch
配置Es：spring.data.elasticsearch.cluster-name=nowcoder，spring.data.elasticsearch.cluster-nodes=127.0.0.1:9300（9200是http端口，9300是tcp端口）

elasticsearch和redis同时依赖于netty，运行冲突，需要在 CommunityApplication.java 加上注解

1
2
3

@PostConstruct
public void init() {		   // 解决netty启动冲突问题
    System.setProperty("es.set.netty.runtime.available.processors", "false");	}

通过ElasticsearchTemplate(底层)，ElasticsearchRwpository(简易) 操作 Es
对实体类加注解，与Es索引、类型、文档、字段映射：@Document(indexName = “”, type = “”, shards = , replicas = )；
配置实体类中的属性：@Id，@Field(type = FieldType.Text, analyzer = “ik_max_word”, searchAnalyzer = “ik_smart”)，，
一种repository对一种实体类做Es操作（区别于@Mapper，mybatis专属的）

// DiscussPostRepository 是对 DiscussPost 做 Es 操作
@Repository                 
public interface DiscussPostRepository 
          extends ElasticsearchRepository<DiscussPost, Integer> {
}            // 只要继承 ElasticsearchRepository，自带save(),delete()等方法

搜索

@Autowired
private DiscussPostRepository discussRepository;
@Autowired
private ElasticsearchTemplate elasticTemplate;
public void saveDiscussPost(DiscussPost post) {
    discussRepository.save(post);             // 先要把（加了注解的）实体类存入 Es
}
public Page<DiscussPost> searchDiscussPost(String keyword, int current, int limit) {
    SearchQuery searchQuery = new NativeSearchQueryBuilder()
            .withQuery(QueryBuilders.multiMatchQuery(keyword, "title", "content")) // 搜索规则
            .withSort(SortBuilders.fieldSort("type").order(SortOrder.DESC))        // 排序规则
            .withPageable(PageRequest.of(current, limit))                          // 分页
            .withHighlightFields(                                                  // 设置高亮
                    new HighlightBuilder.Field("title").preTags("<em>").postTags("</em>"),
            ).build();
    return elasticTemplate.queryForPage(searchQuery, DiscussPost.class, new SearchResultMapper() {
        @Override
        public <T> AggregatedPage<T> mapResults(SearchResponse response, Class<T> aClass, Pageable pageable) {
            // ...
            }
            return new AggregatedPageImpl(...);          }      });  }

Postman

账号：1908454905@qq.com
Postman 是一个流行的 API测试工具和开发环境，它为开发人员提供了一种方便的方式来创建、测试、文档化和共享API。
API 测试： Postman 的主要功能之一是允许用户发送 HTTP 请求以测试 API 端点。您可以创建 GET、POST、PUT、DELETE 等不同类型的请求，并附加参数、标头和正文数据以模拟与 API 交互。
集合和环境： Postman 允许您组织测试请求到集合中。集合是一组相关的请求，可以方便地进行批量执行和管理。您还可以使用环境变量来动态地管理请求中的数据，以便在不同环境中轻松切换。
自动化测试： Postman 提供了测试脚本功能，您可以使用 JavaScript 编写测试脚本，以验证 API 响应是否符合预期。这使得您可以创建自动化测试套件，确保 API 的稳定性和正确性。
协作和共享： Postman 允许用户创建工作空间，多个团队成员可以在同一个工作空间中协作。您还可以共享 Postman 集合和环境，以便其他人可以重复您的测试或使用您的 API。

项目调试技巧

相应状态码：200 - 成功，302 - 重定向（让浏览器再发一个请求），404 - 找不到路径，500 - 服务器遇到问题（服务端有bug）
服务端断点调试：方法中一行代码前打断点，以debug形式启动类。启动服务后，停止在断点处，F8向下执行一步/F7进入方法内部/F9直接执行到下一个断点，观察参数如何变化。
客户端断点调试：在浏览器打开开发者工具，对js文件打断点
设置日志级别，并将日志输出到不同的终端
trace-debug-log-warn-error，按照级别记录日志，动态地启用级别。可以在application.properties配置 logger
或在/resource下放置一个名为logback-spring.xml的文件，自动配置logger（日志存放文件大小、日志类型、存放位置、名字…）

在/test下创建带@Test注解的测试类，直接对某一个mapper/service/..类进行测试。
通过以下注解结合在一起，可以在测试中创建一个与实际应用程序相似的Spring容器，并运行测试。这样可以确保测试能够在实际的Spring环境中运行，并且可以访问和测试应用程序中的各种组件。

1
2
3

@RunWith(SpringRunner.class)  // 此注解用于指定运行测试的运行器，通常与JUnit一起使用。`SpringRunner`是Spring提供的一个JUnit运行器，用于在测试中启用Spring支持。
@SpringBootTest  // 这个注解告诉Spring Boot测试框架要加载整个Spring应用程序上下文，包括所有的bean。它是一个高级版本的`@ContextConfiguration`，它会尝试自动配置Spring应用程序上下文，通常用于集成测试。
@ContextConfiguration(classes = CommunityApplication.class)  // 这个注解用于指定要加载的Spring配置类。在这里，`CommunityApplication.class`是Spring Boot应用程序的主配置类，它包含了应用程序的配置信息。

单元测试

Spring Boot Testing
- 依赖：spring-boot-starter-test
- 包括：Junit、Spring Test、AssertJ、、、
Test Case 测试用例
- 要求：保证测试方法的独立性。
- 步骤：初始化数据、执行测试代码、验证测试结果、清理测试数据。
- 常用注解：@BeforeClass、@AfterClass、@Before、@After。

项目监控

Spring Boot Actuator
- Endpoints：监控应用的入口，Spring Boot内置了很多端点，也支持自定义端点。
- 监控方式：HTTP 或 JMX。
- 访问路径：例如“/actuator/health”
- 注意事项：按需配置暴露的端点，并对所有端点进行权限控制。

性能优化

本地缓存
将数据缓存在应用服务器上，性能最好。如热帖、、
常用缓存工具: Ehcache、Guava、Caffeine等
分布式缓存
将数据缓存在NoSQL数据库上，跨服务器。如登录信息（不管在哪台服务器上都要查得到）
常用缓存工具: MemCache、Redis等.
多级缓存
一级缓存(本地缓存) > 二级缓存(分布式缓存) > DB(避免访问数据库)，每级缓存的内存大小、存储时间都不一样
服务器受到请求，先查看本地缓存，再查redis（分布式缓存），都没有才查DB，同时同步到本地和分布式缓存上
避免缓存雪崩(缓存失效，大量请求直达DB)，提高系统的可用性

Kubernetes

节点：K8s中最小的计算硬件单元。它是集群中单个机器的表示。节点可能是物理机器或者虚拟机，理论上可以是任何东西。
集群：K8s中节点汇聚资源，形成更强大的机器。将程序部署到集群中时，它将智能地处理将工作分配给各个节点。如果添加或删除了任何节点，集群将根据需要在工作中进行转换。这对程序或程序员来说都不重要，因为机器实际上是在运行代码。
Namespace(命名空间, 是一个逻辑隔离的环境,用于资源分组和隔离) -> InfluxDB集群，Pod(Kubernetes的基本计算单元) -> InfluxDB集群节点(逻辑上)，容器 -> InfluxDB单例(物理上，部署在服务器上)
- Pod 是 Kubernetes 中最小的部署单元，一个 Pod 可以包含一个或多个容器。（pod是逻辑概念；容器是物理概念？？存在于物理服务器上）
  K8s 使用控制器（如 Deployment、StatefulSet、DaemonSet 等）来管理 Pod 的生命周期，根据定义的期望状态（如副本数量、更新策略等）来创建、更新和删除 Pod。通过 kubectl 命令可以查看、管理和调试 Pod。
- 容器是运行在 Pod 中的实际应用实例。K8s 使用容器运行时（如 Docker、containerd 等）来管理容器的生命周期。
  每个容器运行一个镜像，容器的配置（如环境变量、挂载卷、资源限制等）在 Pod 的定义中指定。
- 镜像是容器的基础，包含了应用程序及其依赖环境。镜像通常存储在镜像仓库（如 Docker Hub、Google Container Registry 等）中。
虽然 Pod 是 K8s 的基本计算单元，但它们通常不是直接在集群上启动的。相反，Pod 通常由一个抽象层来管理：部署。不必手动处理 Pod，只需声明系统的期望状态，它将自动管理。可以创建一个节点集群，并将Pod部署到集群上。如果需要允许外部通信流进入你的应用程序，与运行在Pod中的服务通信，必须打开一个通信通道，称作入口(ingress)。
关于 InfluxDB 集群的部署和通信：
- 部署方式：对于一个命名空间下的几个Pod，这些节点会通过 StatefulSet 或者 Deployment 来进行管理和部署。
- 调度到主机：K8s 的调度器会根据资源需求、节点的可用资源以及调度策略（如反亲和性、亲和性等）来决定 Pod 部署到哪台主机上。你可以使用以下命令查看 Pod 所在的节点信息：kubectl get pod -n influxdb -o wide
- 通信调度：K8s 中，Pod 之间的通信通常通过 Service 来进行。Service 会为一组 Pod 提供一个稳定的 IP 地址和 DNS 名称。对于 InfluxDB 集群，可能会有一个或多个 Service 来管理数据节点和元数据节点之间的通信。你可以使用以下命令查看 InfluxDB 命名空间中的 Service：kubectl get svc -n influxdb

2020-09-08

数组 / 链表 / 哈希表 / 字符串 / 栈 / 队列 / 二叉树 / 图 / 贪心 / 回溯 / 动态规划

数组

二分查找

二分查找： 前提是数组为有序数组，同时题目还强调数组中无重复元素。想清楚对区间的定义，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。
写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。

int search(vector<int>& nums, int target) {                     // 第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要非常重要）。
    int left = 0, right = nums.size()-1; 
    while (left <= right) {                                     // 要使用 <= ，因为left == right有意义
        int middle = left + (right - left) / 2;                 // 避免left + right溢出
        if (nums[middle] > target) { right = middle - 1; }      // 因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1
        else if (nums[middle] < target) { left = middle + 1; } 
        else { return middle;} 
    }
    return -1;                                                  // 当right < left，说明不存在targrt
}

二分查找第一个位置： 找出给定目标值在数组中的第一个位置（和结束位置）。

int l = 0, r = nums.length - 1;
int first = -1;
while(l <= r) {
    int i = (l + r)/ 2;
    if(nums[i] == target) {
        r = i - 1;
        first = i;   // 重点, 如果找最后一个位置的话就是 l = i + 1;
    } else if(nums[i] < target) {
        l = i + 1;
    }else {
        r = i - 1;
    }
}

二分查找插入 ：在排序数组中寻找是否存在一个目标值，且如果不存在数组中的时候需要返回按顺序插入的位置。可以将两个条件合并得出最后的目标：「在一个有序数组中找第一个大于等于 target 的下标」，此时需要对二分法稍作修改，不断用二分法逼近查找第一个大于等于 target 的下标。

class Solution {
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;
        int left = 0, right = n - 1;
        while (left <= right) {
            int mid = ((right - left) >> 1) + left;
            if (nums[mid] >= target) 
                right = mid - 1;
            else left = mid + 1;
        }
        return l;
    }
}

x 的平方根
1

双指针

原地移除 （快慢指针法）通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。（前后指针）
给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。

int removeElement(vector<int>& nums, int val) {
    int slow = 0;
    for (int fast = 0; fast < nums.size(); fast++) {
        if (nums[fast] != val) {       // 此时快指针指向 新数组（原数组去除了val）中的元素
            nums[slow] = nums[fast];   // 用慢指针，直接在原数组的基础上得到去除了 val 的新数组
            slow++;
        }
    }
    return slow;
}

盛最多水的容器：给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
初始化：双指针 i, j 分列水槽左右两端；循环收窄：选定两板高度中的短板，向中间收窄一格，同时更新面积最大值 res，直至双指针相遇时跳出。
两数之和II ：

滑动窗口

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，用一个for循环代替两个for循环的功能实现，从而将O(n^2)暴力解法降为O(n)。只用一个for循环，那么这个循环的索引，一定是表示滑动窗口的终止位置，问题是如何移动滑动窗口的起始位置。

最小连续子数组： 找出数组中满足其和 ≥ target 的长度最小的连续子数组并返回其长度

int minSubArrayLen(int target, vector<int>& nums) {   
    int i = 0, j = 0, sum = 0, ans = INT_MAX ;        // i 滑动窗口起始位置，j 滑动窗口结束位置，当前活动窗口内和
    for (; j < nums.size(); j++) {
        sum = sum + nums[j];                          // j 后移
        while (sum >= target) {
            ans = (j - i + 1) < ans ? (j - i + 1) : ans;
            sum = sum - nums[i++];                    // i 前移
        }
    }         // ！！！ O(n):不要以为for里放一个while就以为是O(n^2)啊，主要是看每一个元素被操作的次数，每个元素在滑动窗后进来操作一次，出去操作一次，每个元素都是被操作两次，所以时间复杂度是 2 × n 也就是O(n)。
    return ans == INT_MAX ? 0 : ans;                 // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
}

模拟实现

数组是非常基础的数据结构，在面试中，考察数组的题目一般在思维上都不难，主要是考察对代码的掌控能力。
螺旋数组，打印数组。。。

链表

链表操作中的头结点处理：在 Java 中，处理链表的头结点可以直接使用原始链表进行删除操作，也可以采用设置虚拟头结点的方式进行操作。虚拟头结点是一个不存储任何实际数据的头结点，它可以简化链表操作，避免对头结点进行特殊处理。
需要用到头结点时，使用 ListNode* cur = head 进行链表操作，不要直接使用头结点操作！！！
空指针的判断：使用 if (ptr != null) 来判断一个对象是否为空。Java 中的空指针用 null 关键字（不是一个宏定义）表示，而不是像 C++ 中的 nullptr。

设计链表： 设计节点的结构，链表的结构和五个函数：

class MyLinkedList {
    class ListNode {  // 设计链表中节点的数据结构
        int val;      // 节点上存储的元素
        ListNode next; // 指向下一个节点的指针

        ListNode(int x) {  // 节点的构造函数
            val = x;
            next = null;
        }
    }

    ListNode dummyhead; // 虚拟（假）头结点
    int size;           // 记录链表长度，在add, delete操作前进行判断

    public MyLinkedList() {
        dummyhead = new ListNode(0);
        size = 0;
    }

    public int get(int index) { // 获取链表中第 index 个节点的值。如果索引无效，则返回-1。
        if (index < 0 || index >= size) return -1;
        ListNode cur = dummyhead.next;
        while (index-- > 0) {
            cur = cur.next;
        }
        return cur.val;
    }

    public void addAtHead(int val) { // 在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
        ListNode cur = new ListNode(val);
        cur.next = dummyhead.next;
        dummyhead.next = cur;
        size++;
    }

    public void addAtTail(int val) { // 将值为 val 的节点追加到链表的最后一个元素
        ListNode cur = dummyhead;
        ListNode tail = new ListNode(val);
        while (cur.next != null) {
            cur = cur.next;
        }
        cur.next = tail;
        size++;
    }

    public void addAtIndex(int index, int val) { // 在链表中的第 index 个节点之前添加值为 val  的节点。
        if (index < 0) {  // 根据下标判断插入位置
            addAtHead(val);
        } else if (index == size) {
            addAtTail(val);
        } else if (index > size) {
            return;
        } else {
            ListNode cur = dummyhead;
            ListNode node = new ListNode(val);
            while (index-- > 0) {
                cur = cur.next;
            }
            node.next = cur.next;
            cur.next = node;
            size++;
        }
    }

    public void deleteAtIndex(int index) { // 如果索引 index 有效，则删除链表中的第 index 个节点。
        if (index < 0 || index >= size) return;
        ListNode cur = dummyhead;
        while (index-- > 0) {
            cur = cur.next;
        }
        ListNode nex = cur.next.next;
        cur.next = nex;
        size--;
    }
}

链表翻转：
环：相遇
1.判断有无环：定义快慢指针，慢的先走，快的后走，一次一步。若有环，快指针必然追上满指针，且相遇位置必然在环内。
2.确定环的入口：定义两个指针，一个位于链表头指针，一个位于快慢指针相遇位置。这两个指针每次只走一个节点，那么当这两个指针相遇的时候就是环形入口的节点。

哈希表

在 Java 中，哈希（Hash）是将数据映射到固定大小的散列值的技术。哈希函数用于将输入数据转换为散列值，通常用于快速查找或存储数据。通过调用对象的 hashCode() 方法获得数据的散列码（hash code）。同时，Java 中也提供了 java.util.Objects 类，其中包含了 hash() 方法，用于计算对象的哈希值。
Java 的标准库提供了 java.util 包中的一些类和接口，比如 HashMap、HashSet 等。
什么时候使用哈希法？当我们需要查询一个元素是否出现过，或者一个元素是否在集合里的时候，就要第一时间想到哈希法。
四数之和II： 四个数组各组一个元素，四元素和为0。找出四数的不同组合个数。
两个哈希表：map1，map2，分别记录 num1与num2 各种组合的和的个数，num3与num4 各种组合的和的个数
for(auto pair : map1)，若 map2[0 - pair.first] 存在，则 ans += pair.second * map2[0 - pair.first]

三数之和： 一个数组，找出其中三个元素和为0。找出所有不重复的三元组。
一层循环（a） + 每层循环中双指针（b，c）

vector<vector<int>> threeSum(vector<int>& nums) {
    vector<vector<int>> ans;
    sort(nums.begin(), nums.end());                          // 首先将数组排序
    for(int i = 0; i < nums.size() - 2; i++) {               // 一层for循环（a）
        if (nums[i] > 0)  break; 
        if (i>0 && nums[i]==nums[i-1])  continue;            // 去重a！！！    
        int left = i + 1;                                    // 循环内定义双指针（b，c）
        int right = nums.size() - 1;
        while (left < right) {                               // 循环条件！！
            // 不要在这里直接先去重b，c，免得一个答案都没有
            if (nums[i] + nums[left] + nums[right] == 0) {
                ans.push_back({nums[i], nums[left], nums[right]});  
                // 一定要先执行上一句代码，即先找到一个答案 【0,0,0,0,0】
                // 再去执行下两句，去重b，c！！！    
                while (left<right && nums[left]==nums[left+1])    left++;
                while (left<right && nums[right]==nums[right-1])  right--;
                // 找到答案，左右指针同时收缩 【-2，0，0,2,2】
                left++;
                right--;
            } else if (nums[i] + nums[left] + nums[right] < 0)     left++;
              else if (nums[i] + nums[left] + nums[right] > 0)     right--; 
        }
    }
    return ans;
}

四数之和： 和三数之和是一个思路，都是使用双指针法, 基本解法就是在三数之和的基础上再套一层for循环。
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值，依然是循环内有left和right下标作为双指针，找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况，三数之和的时间复杂度是O(n^2)，四数之和的时间复杂度是O(n^3) 。

字符串

Java 中并没有像 Cpp中的 getline 函数，而是可以使用 Scanner 或者 BufferedReader 从控制台读取一行文本。

import java.util.Scanner;
// ...
Scanner scanner = new Scanner(System.in);
String line = scanner.nextLine(); // ...
scanner.close();

1
2
3

BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
String line = reader.readLine();
reader.close();

翻转字符串里的单词： 移除多余空格、将整个字符串反转、将每个单词反转
移除多余空格：参考快慢指针原地去除数组特定元素的方法（题目见）
翻转问题：考虑 部分翻转 + 整体翻转
同构字符串：需要我们判断 s 和 t 每个位置上的字符是否都一一对应，即 s 的任意一个字符被 t 中唯一的字符对应，同时 t 的任意一个字符被 s 中唯一的字符对应。这也被称为「双射」的关系。
因此，我们维护两张哈希表，第一张哈希表 s2t 以 s 中字符为键，映射至 t 的字符为值，第二张哈希表 t2s 以 t 中字符为键，映射至 s 的字符为值。从左至右遍历两个字符串的字符，不断更新两张哈希表，如果出现冲突（即遍历 s 当前下标 i 已经存在映射 s2t.get(s.charAt(i)) 且不为 t.charAt(i)，或遍历 t 当前下标 i 已经存在映射 t2s.get(t.charAt(i)) 且不为 s.charAt(i)）说明两个字符串无法构成同构，返回 false

KMP模式匹配： 当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。
子串和主串匹配出现冲突 -> 寻找子、主串匹配冲突位置前部分的最长相等前后缀（查冲突位置前一位在前缀表中的值[next数组]） -> 子串匹配位置返回到相等前缀后一位（即冲突位置在next中的值），主串匹配位置不移动（也即返回到相等后缀后一位），再次开始匹配。

void getNext(int* next, const string& s) {      // 1. 利用模式串s，构造前缀表next
    int j = 0;                                  // （若j为 -1，前缀表要进行统一减一的操作）
    next[0] = 0;                                // next[i] 表示 i（包括i）之前最长相等的前后缀长度
    for(int i = 1; i < s.size(); i++) {         // 注意i从1开始
        while (j > 0 && s[i] != s[j]) {         // j前后缀不相同了（要保证大于0，因为下面有取j-1作为数组下标的操作
            j = next[j - 1];                    // 向前回退（注意这里，是要找前一位的对应的回退位置了
        }
        if (s[i] == s[j]) {                     // 找到相同的前后缀
            j++;
        }
        next[i] = j;                            // 将j（前缀的长度）赋给next[i]
    }
}

int strStr(string haystack, string needle) {        // 2. 用模式串needle 匹配主串haystack 
    if (needle.size() == 0)  return 0;
    int next[needle.size()]; 
    getNext(next, needle);                          // 用模式串创建next数组 O(n)
    int j = 0;                                      // 模式串中当前匹配位置
    for (int i = 0; i < haystack.size(); i++) {     // O(m)，则KMP算法为O(m+n)
        while(j > 0 && haystack[i] != needle[j]) {  // 不匹配，j 寻找之前匹配的位置
            j = next[j - 1];                        
        }
        if (haystack[i] == needle[j]) {             // 匹配，j和i同时向后移动
            j++;
        }
        if (j == needle.size() ) {                  // 文本串s里出现了模式串t
            return (i - needle.size() + 1);
        }
    }
    return -1;
}

栈与队列

匹配问题都是栈的强项： 括号匹配，相邻元素匹配，逆波兰式匹配（注意后从栈中弹出的数，是操作符的左操作数），，

滑动窗口最大值： 给定数组 nums，有大小为 k 的滑动窗口从数组的最左侧一位位移向最右侧。每次返回滑动窗口中的最大值。
单调队列：维护一个单调递增（减）的队列，最大（小）值在队首。单调队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小（小到大）的。具体做法是：
pop()时：若要从滑动窗口中去掉的元素，其值等于此时单调队列队首值（即最大值），那么将队首元素从deque.front()弹出。滑动窗口每次向右滑动，先pop()，后push()。
push()时：从双向队列末尾push数值，若大于前面的数，那么将前面的数从deque.back()弹出，直到push的数值小于等于其前面元素的数值为止。这样就保持了队列里的数值是单调从大到小的了，且最大值在队首deque.front()。

class MyQueue { 
public:                 // !!！ 注意别漏了public，否则默认private无法从变量访问
    deque<int> que; 
    void pop(int value) {
        if (!que.empty() && value == que.front()) {
            que.pop_front();
        }
    }
    void push(int value) {
        while (!que.empty() && value > que.back()) {
            que.pop_back();
        }
        que.push_back(value);

    }
    int front() { return que.front();  }
};

前 K 个高频元素： 给定一个非空的整数数组，返回出现频率前 k 高的元素。
优先级队列：其实就是一个披着队列外衣的堆，对外接口只是从队头取元素，从队尾添加元素，且优先级队列内部元素是自动依照元素的权值排列。 缺省情况下priority_queue利用max-heap（大顶堆）完成对元素的排序，这个大顶堆是以vector为表现形式的complete binary tree（完全二叉树）。
堆 是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。每次pop()弹出堆顶元素。
priority_queue：c++中已实现的数据结构，其底层实现等同于堆，从小到大排就是小顶堆，从大到小排就是大顶堆。

class mycomparison {                // 小顶堆
public:
    bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
        return lhs.second > rhs.second;
    } 
};                    
unordered_map<int, int> map;        // 要统计元素出现频率                  
for (int i = 0; i < nums.size(); i++) {
    map[nums[i]]++; }
// 对频率排序, 维护一个大小固定为k的小顶堆，扫面所有频率的数值
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;  
for (auto pair : map) {
    pri_que.push(pair);
    if (pri_que.size() > k) {       // 如果堆的大小大于了K，则队列弹出，保证堆的大小一直为k
        pri_que.pop();
    }
}

`LinkedList`（双向链表）

在 Java 中，LinkedList 是双向链表的实现，每个元素都包含一个指向前一个元素和一个指向后一个元素的指针。这使得插入和删除操作在链表中非常高效，但随机访问较慢。以下是 LinkedList 的一些常见用法：

import java.util.LinkedList;

public class Main {
    public static void main(String[] args) {
        LinkedList<Integer> myList = new LinkedList<>();
        myList.addLast(1);                          // 插入元素到链表尾部
        myList.addFirst(2);                         // 插入元素到链表头部
        myList.add(1, 3);                           // 在指定位置插入元素
        myList.removeLast();                        // 移除链表尾部元素
        myList.removeFirst();                       // 移除链表头部元素
        myList.remove(1);                            // 移除指定位置的元素
        for (int item : myList) { System.out.print(item + " "); } // 遍历链表
    }
}

`Deque`（双端队列）

Deque 是双端队列容器的实现，支持在两端进行高效的插入和删除操作，并且允许随机访问。

import java.util.Deque;
import java.util.ArrayDeque;

public class Main {
    public static void main(String[] args) {
        Deque<Integer> myDeque = new ArrayDeque<>();
        myDeque.addLast(1);                         // 插入元素到队列尾部
        myDeque.addFirst(2);                        // 插入元素到队列头部
        myDeque.removeLast();                       // 移除队列尾部元素
        myDeque.removeFirst();                      // 移除队列头部元素
        myDeque.addLast(3);                         // 随机访问队列
        myDeque.addLast(4);
        int value = myDeque.peekFirst();            // 访问第一个元素
        for (int item : myDeque) { System.out.print(item + " "); } // 遍历队列
    }
}

`PriorityQueue`（优先队列）

在 Java 中，PriorityQueue 可以实现最大堆和最小堆。默认情况下是最小堆，可通过提供自定的比较器来实现最大堆或最小堆。

import java.util.PriorityQueue;
// 实现最大堆：
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a); // 创建最大堆
maxHeap.offer(5);  maxHeap.offer(2);  maxHeap.offer(8);  maxHeap.offer(1); // 向堆中插入元素
System.out.println("最大值：" + maxHeap.peek()); // 访问堆顶元素（最大值）
maxHeap.poll(); // 弹出堆顶元素

// 实现最小堆：
PriorityQueue<Integer> minHeap = new PriorityQueue<>(); // 创建最小堆
minHeap.offer(5);  minHeap.offer(2);  minHeap.offer(8);  minHeap.offer(1); // 向堆中插入元素
System.out.println("最小值：" + minHeap.peek()); // 访问堆顶元素（最小值）
minHeap.poll(); // 弹出堆顶元素

二叉树

满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则为满二叉树。
完全二叉树：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点。
优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。
二叉搜索树 BST：具有有序性质，适用于快速查找、插入和删除操作。
若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树
平衡二叉搜索树 AVL： 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

`递归（traversal）三要素`: 确定递归函数的参数和返回值 -> 确定终止条件 -> 确定单层递归的逻辑

深度优先遍历：
前序遍历（递归法，迭代法），中序遍历（递归法，迭代法），后序遍历（递归法，迭代法）
也可以利用栈实现迭代形式的遍历。

广度优先遍历：
层序遍历（迭代法）一个二叉树。就是从左到右一层一层的去遍历二叉树。借用队列来实现。
学会二叉树的层序遍历，可以一口气打下十题：二叉树的右视图，二叉树的层平均值，在每个树行中找最大值，填充每个节点的下一个右侧节点指针，填充每个节点的下一个右侧节点指针II，二叉树的最大深度，二叉树的最小深度，，，

void traversal(TreeNode* cur, vector<int>& vec) { // 前序遍历（递归法）
    if (cur == NULL) return;
    vec.push_back(cur->val);                      // 先 中间节点
    traversal(cur->left, vec);                    // 再 左子树
    traversal(cur->right, vec);                   // 再 右子树
}
vector<int> preorderTraversal(TreeNode* root) {   // 前序遍历（迭代法）
    stack<TreeNode*> st;                          // 中、后序遍历的迭代法无法与之简单类比，但存在统一迭代法
    vector<int> result;
    if (root == NULL) return result;
    st.push(root);
    while (!st.empty()) {
        TreeNode* node = st.top();                 // 中
        st.pop();
        result.push_back(node->val);
        if (node->right) st.push(node->right);     // 右（空节点不入栈）
        if (node->left)  st.push(node->left);      // 左（空节点不入栈）
    }                                              // 要先加入右孩子再加入左孩子呢,这样出栈的时候才是中左右的顺序。
    return result;
}

vector<vector<int>> levelOrder(TreeNode* root) {   // 层序遍历模板
    queue<TreeNode*> que;
    if (root != NULL) que.push(root);
    vector<vector<int>> result;
    while (!que.empty()) {
        int size = que.size();
        vector<int> vec;
        for (int i = 0; i < size; i++) {  // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            TreeNode* node = que.front();
            que.pop();
            vec.push_back(node->val);
            if (node->left) que.push(node->left);
            if (node->right) que.push(node->right);
            // for(int i = 0; i < node->children.size(); i++) {  // 如果有多个孩子节点
            //    if(node->children[i]) que.push(node->children[i]) }
        }
        result.push_back(vec);
    }
    return result;
}

翻转二叉树： 前序遍历，翻转左右子树，翻转左、右子树的左右子树。

平衡二叉树： 同时操作两个二叉树。判断对称二叉树不是比较左右节点，要比较的是根节点的左子树与右子树是不是相互翻转的，即其实我们要比较的是两个树（这两个树是根节点的左右子树）

bool compare(TreeNode* left, TreeNode* right) {
    // 首先排除空节点的情况、数值不相同的情况
    if ((left == NULL && right != NULL)||(left != NULL && right == NULL)) return false;
    else if (left == NULL && right == NULL) return true;
    else if (left->val != right->val) return false;
    // 左右节点都不为空，且数值相同的情况; 此时才做递归，做下一层的判断
    bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右
    bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左
    return outside && inside;                           // 左子树：中、 右子树：中 （逻辑处理）
}

二叉树最大深度： 二叉树的最大深度就是根节点的最大深度。一个节点的最大深度 = max{ 左孩子的最大深度，右孩子的最大深度 }
1
2
3
int maxDepth(TreeNode* root) {
if (root == null) return 0;
return 1 + max(maxDepth(root->left), maxDepth(root->right)); }

二叉树最小深度： 不能简单地认为一点的最小深度为 1 + min{左,右孩子的深度}，要从根到叶子节点的路径才能算一个深度值。（根到一个中间节点，其某一孩子为空指针，的路径不算一个深度）

int traversal(TreeNode* root) {
    if(!root) return 0;
    if(!root->left && !root->right) return 1;
    if(!root->left)  return 1 + traversal(root->right);
    if(!root->right) return 1 + traversal(root->left);
    return 1 + min(traversal(root->left), traversal(root->right)); }

二叉搜索树： 二叉搜索树可是有序的。遇到在二叉搜索树上求什么最值啊，差值之类的，就把想成在它通过中序遍历转换成的一个有序数组上求最值，求差值，，
二叉搜索树中的众数： 遍历+双指针，，，，

从前序与中序遍历序列构造二叉树： 给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

Map<Integer, Integer> indexMap;
// 每次结合preorder和inorder数组确定一个根节点（画图看很清晰）
public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, 
                int inorder_left, int inorder_right) {
    if (preorder_left > preorder_right) return null;
    TreeNode root = new TreeNode(preorder[preorder_left]);
    int inorderIndex = indexMap.get(preorder[preorder_left]);
    int leftSize = inorderIndex - inorder_left;     
    // 递归地确定当前根节点的左右子树的根节点
    root.left = myBuildTree(preorder, inorder, preorder_left+1, preorder_left+leftSize, inorder_left, inorderIndex-1);
    root.right = myBuildTree(preorder, inorder, preorder_left+leftSize+1, preorder_right, inorderIndex+1, inorder_right);
    return root;
}
public TreeNode buildTree(int[] preorder, int[] inorder) {
    indexMap = new HashMap<>();
    int n = inorder.length;
    // 记录当前根节点（preorder数组第一位）在inorder数组中的位置
    for(int i = 0; i < n; i++) indexMap.put(inorder[i], i);
    return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
}

二叉树求最小公共祖先： 需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从底向上的遍历方式。
在回溯的过程中，必然要遍历整棵二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) { // 递归结束条件
            return root;
        }

        // 后序遍历
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);

        if(left == null && right == null) { // 若未找到节点 p 或 q
            return null;
        }else if(left == null && right != null) { // 若找到一个节点
            return right;
        }else if(left != null && right == null) { // 若找到一个节点
            return left;
        }else { // 若找到两个节点
            return root;
        }
    }
}

图

深度优先搜索（DFS）

DFS从起始节点开始，沿着一条路径一直访问到最深处，然后回溯到上一层，继续访问其他路径。它通过递归或栈实现，保证深度遍历直到底部，然后回溯继续探索其他路径。

dfs的代码框架: （其实dfs就是回溯，其实二叉树的前中后序遍历就是dfs）

void dfs(参数) {           
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本节点所连接的其他节点) {
        处理节点;
        dfs(图，选择的节点); // 递归
        回溯，撤销处理结果
    }
}

所有可能的路径： 给你一个有 n 个节点的有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）。 graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

List<List<Integer>> ans;  // 结果路劲列表
List<Integer> path;       // 当前路劲
// index表示从当前深搜到哪个节点
public void dfs(int[][] graph, int index) {
    if(index == (graph.length - 1)) {
        ans.add(new ArrayList<>(path));  // ！！不要ans.add(path); 否则加入的是引用的同一个对象
        return;
    }
    for(int i = 0; i < graph[index].length; i++) {
        path.add(graph[index][i]);
        dfs(graph, graph[index][i]);
        path.remove(path.size() - 1);
    }
}
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
    path = new ArrayList<Integer>();
    ans = new ArrayList<List<Integer>>();
    path.add(0);
    dfs(graph, 0);
    return ans;
}

广度优先搜索（BFS）

BFS从起始节点开始，依次访问其邻居节点，然后访问邻居节点的邻居，以此类推。它通过队列实现，保证先访问离起始节点近的节点，再访问离起始节点远的节点。

广搜代码模板：（该模板针对的是四方格地图模型）

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图，也就是一个二维数组
// visited 标记访问过的节点，不要重复访问
// x, y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
    queue<pair<int, int>> que;                       // 定义队列
    que.push({x, y});                                // 起始节点加入队列
    visited[x][y] = true;                            // 只要加入队列，立刻标记为访问过的节点
    while(!que.empty()) {                            // 开始遍历队列里的元素
        pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
        int curx = cur.first;
        int cury = cur.second;                       // 当前节点坐标
        for (int i = 0; i < 4; i++) {                // 开始想当前节点的四个方向左右上下去遍历
            int nextx = curx + dir[i][0];
            int nexty = cury + dir[i][1];            // 获取周边四个方向的坐标
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size())
                continue;                            // 坐标越界了，直接跳过
            if (!visited[nextx][nexty]) {            // 如果节点没被访问过
                que.push({nextx, nexty});            // 队列添加该节点为下一轮要遍历的节点
                visited[nextx][nexty] = true;        // 只要加入队列立刻标记，避免重复访问
            }
        }
    }
}

贪心算法

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。
难点就是如何通过局部最优，推出整体最优。靠自己手动模拟，如果模拟可行就可以试一试贪心策略，如果不可行可能需要动态规划。
如何验证可不可以用贪心算法呢？最好用的策略就是举反例，如果想不到反例，那么就试一试贪心吧。
如果需要严格的数学证明，一般有两种方法：数学归纳法、反证法。
可以说：刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。

贪心一般解题步骤

一般分为如下四步：
1.将问题分解为若干个子问题 2. 找出适合的贪心策略 3. 求解每一个子问题的最优解 4. 将局部最优解堆叠成全局最优解
这个四步其实过于理论化了，，，做题的时候，只要想清楚局部最优是什么，如果推导出全局最优，其实就够了。

最大子序和： 给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
示例：输入 [-2,1,-3,4,-1,2,1,-5,4]，输出 6。解释: 连续子数组 [4,-1,2,1] 的和最大，为 6
解答：直接遍历一路加过去就行，记录目前的“连续和”以及最大“连续和”，当目前的“连续和”为负数时置0，“重新”开始计算“连续和”。
局部最优：当前“连续和”为负数的时候立刻放弃，从下一个元素重新计算“连续和”，因为负数加上下一个元素 “连续和”只会越来越小。全局最优：选取最大“连续和”
摆动序列：
买卖股票的最佳时机 II： 给定股票每天的价格，计算所能获取的最大利润，可以尽可能地完成更多的交易（多次买卖一支股票）。在每一天，你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。
解答：想到选一个低的买入，再选个高的卖，再选一个低的买入…..循环反复。即最终利润是可以分解的，把利润分解为每天为单位的维度，而不是从 0 天到第 n 天整体去考虑，那么根据 prices 可以得到每天的利润序列：(prices[i] - prices[i - 1])…..(prices[1] - prices[0])。最大利润就是取其中的所有正值之和。
跳跃游戏 II：
加油站：环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。从其中的一个加油站出发，开始时油箱为空。如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。
解答：首先如果总油量减去总消耗大于等于零，那么一定可以跑完一圈，即各个站点的加油站剩油量rest[i]=gas[i] - cost[i] 相加之和一定是大于等于零的。令 i 从0开始累加 rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，因为这个区间选择任何一个位置作为起点，到i这里都会断油，那么起始位置从i+1算起，再从0计算curSum。
局部最优：当前累加rest[i]的和curSum一旦小于0，起始位置至少要是i+1，因为从i之前开始一定不行。全局最优：找到可以跑一圈的起始位置。

分发糖果：ratings[] 表示每个孩子的评分。你需要按照以下要求，给这些孩子分发糖果：1、每个孩子至少分配到 1 个糖果。2、相邻两个孩子评分更高的孩子会获得更多的糖果。
解答：这道题目一定是要确定一边之后，再确定另一边，例如比较每一个孩子的左边，然后再比较右边，如果两边一起考虑一定会顾此失彼。先确定右边评分大于左边的情况（也就是从前向后遍历）只要右边评分比左边大，右边的孩子就多一个糖果；再确定左孩子大于右孩子的情况（从后向前遍历）只要左边评分比右边大，左边的孩子就多一个糖果。

for(int i = 1; i < n; i++) {
    if(ratings[i] > ratings[i-1])  candys[i] = candys[i-1] + 1;
}
for(int i = n-2; i >= 0; i--) {
    if(ratings[i] > ratings[i+1]) {
        // 此时candyVec[i]（第i个小孩的糖果数量）就有两个选择了，一个是candyVec[i + 1] + 1（从右边这个加1得到的糖果数量），一个是candyVec[i]（之前比较右孩子大于左孩子得到的糖果数量），取最大值。
        // 即局部最优：取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优：相邻的孩子中，评分高的孩子获得更多的糖果。
        candys[i] = max(candys[i], candys[i+1] + 1);
    }
}

回溯算法

回溯法也可以叫做回溯搜索法，它是一种搜索的方式。回溯是递归的副产品，只要有递归就会有回溯。
回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作。
回溯法解决的问题都可以抽象为树形结构，所有回溯法的问题都可以抽象为树形结构！
因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

`回溯（backtracking）三步曲`：回溯函数模板返回值及参数 -> 函数终止条件 -> 回溯搜索的遍历过程

回溯函数模板：

void backtracking(参数) {             
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表);  // 递归
        回溯，撤销处理结果
    }
}

组合问题： 给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合;
示例: 输入: n = 4, k = 2 输出: [ [1,2], [1,3], [1,4], [2,3],[2,4], [3,4] ]

class Solution {                        
private:
    vector<vector<int>> result;                       // 存放符合条件结果的集合
    vector<int> path;                                 // 用来存放符合条件结果
    void backtracking(int n, int k, int startIndex) { // startIndex记录下一层递归，搜索的起始位置
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n; i++) {   // 控制树的横向遍历
            path.push_back(i);                    // 处理节点
            backtracking(n, k, i + 1);            // 递归：控制树的纵向遍历，注意下一层搜索从i+1开始
            path.pop_back();                      // 回溯，撤销处理的节点
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }
};

子集问题： 给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。说明：解集不能包含重复的子集。
示例: 输入: nums = [1,2,3] 输出: [ [], [1], [1, 2], [1,2,3], ]
如果把子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！

分割回文串： 给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。
示例: 输入: “aab” 输出: [ [“aa”,”b”], [“a”,”a”,”b”] ]
其实切割问题类似组合问题，例如对于字符串abcdef：
组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个…..。
切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段…..。

！！！一定建立起for循环横向遍历，递归纵向遍历的概念！！！

void backtracking(string s, int startindex) {
    if (startindex >= s.size()) {   // 0.终止条件_遍历到“叶子结点”，一组成功样例                               
        ans.push_back(path);
        return;
    }
    for (int i = startindex; i < s.size(); i++) {
        if (ishuiwen(s.substr(startindex, i - startindex + 1))) {   
            path.push_back(s.substr(startindex, i - startindex + 1));
        } else {                    
            continue;               // 1.处理节点：切割startindex~i的子串
        }                           // ！！不要在终止条件里处理节点！！
        backtracking(s, i + 1);     // 2.处理完节点后遍历  
        path.pop_back();            // 3.回溯 
    }
}

排列问题： 给定一个没有重复数字的序列，返回其所有可能的全排列。排列是有序的，即[1,2] 和 [2,1] 是两个集合。
示例：输入[1,2,3]，输出 [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

public:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking (vector<int>& nums, vector<bool>& used) {
        if (path.size() == nums.size()) {
            result.push_back(path);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {     
            // 元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1
            // 所以处理排列问题不使用startIndex，i从0开始遍历。
            if (used[i] == true) continue;   // path里已经收录的元素，直接跳过
            used[i] = true;
            path.push_back(nums[i]);
            backtracking(nums, used);
            path.pop_back();
            used[i] = false;
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        // used数组，其实就是记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次。
        vector<bool> used(nums.size(), false);      
        backtracking(nums, used);
        return result;
    }

hhh

动态规划

动态规划，Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的。
动态规划算法一般分为自顶向下的记忆化搜索和自底向上的递推方法。自顶向下方法使用递归来解决问题，但在递归过程中使用记忆数组（或哈希表）来保存已经计算过的子问题的解，以避免重复计算。自底向上方法则从子问题的基础解逐步构建出问题的解。(递归到动规的一般转化方法：递归函数有n个参数，就定义一个n维的数组，数组的下标是递归函数参数的取值范围，数组元素的值是递归函数的返回值，这样就可以从边界值开始，逐步填充数组，相当于计算递归函数值的逆过程。)
动态规划通常适用于具备以下特点的问题：
1. 重叠子问题： 问题的解可以由多个子问题的解组合而来，这些子问题可能会被重复解决。
2. 最优子结构： 问题的最优解可以通过其子问题的最优解构造得到。
3. 无后效性： 当前的若干个状态值一旦确定，则此后过程的演变就只和这若干个状态的值有关，和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态，没有关系。

`动态（DP）规划五步曲` 1. 确定dp数组（dp table）以及下标的含义 -> 2. 确定递推公式 -> 3. dp数组如何初始化 -> 4. 确定遍历顺序 -> 5. 举例推导dp数组

01背包问题： 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
1.dp数组以及下标含义：使用二维数组dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。
2.递推公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以背包内的价值依然和前面相同。)
放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值
3.dp数组初始化：关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

4.遍历顺序：先遍历物品、先遍历背包重量都可以。把dp表遍历填满就行。
5.举例推导dp：做动态规划的题目，最好的过程就是自己在纸上举一个例子把对应的dp数组的数值推导一下，然后在动手写代码！

void test_2_wei_bag_problem1() {
    int bagweight = 4; 
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30}; 
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));   // 二维数组
    for (int j = weight[0]; j <= bagweight; j++)  dp[0][j] = value[0];      // 初始化
    for (int i = 1; i < weight.size(); i++) {                               // 遍历物品
        for (int j = 0; j <= bagweight; j++) {                              // 遍历背包容量
            if (j < weight[i]) dp[i][j] = dp[i - 1][j];
            else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        }
    } 
    cout << dp[weight.size() - 1][bagweight] << endl;
}

打家劫舍： 每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组，计算你不触动警报装置的情况下，一夜之内能够偷窃到的最高金额。
1.dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]。
2.dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])；决定dp[i]的因素就是第i房间偷还是不偷。
如果偷第i房间，那么dp[i] = dp[i - 2] + nums[i] ，即：第i-1房一定是不考虑的，找出下标i-2（包括i-2）以内的房屋，最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。
如果不偷第i房间，那么dp[i] = dp[i - 1]，即考虑 i-1 房，（注意这里是考虑，并不是一定要偷i-1房！）
3.dp数组初始化：递推公式的基础就是dp[0] 和 dp[1]；dp[0] 一定是 nums[0]，dp[1]就是nums[0]和nums[1]的最大值
4.遍历顺序：dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的，那么一定是从前到后遍历！
5.举例推导dp数组
打家劫舍II： 房子首尾相连。
情况一：考虑不包含首尾元素；情况二：考虑包含首元素，不包含尾元素；情况三：考虑包含尾元素，不包含首元素
答案即情况二、三之间的大的值
最长递增子序列：找到整数数组 nums 中最长严格递增子序列的长度。例如，[3,6,2,7] 是 [0,3,1,6,2,2,7] 的子序列。
定义 dp[i] 为考虑前 i 个元素，以第 i 个数字结尾的最长上升子序列的长度，注意 nums[i] 必须被选取！！！
1
2
3
for(int i = 1; i < n; i++) {
for(int j = 0; j < i; j++) {
if(nums[i] > nums[j] && (1 + dp[j]) > dp[i]) dp[i] = dp[j] + 1; // 返回dp[]最大值 }}
股票问题： 给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择某一天买入这只股票，并选择在未来的某一个不同的日子卖出该股票。设计一个算法来计算你所能获取的最大利润。
dp[i][0] 表示第i天持有股票所得最多现金；dp[i][1] 表示第i天不持有股票所得最多现金。
dp[i][0] = max(dp[i - 1][0], -prices[i]); dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
子序列问题：

单词拆分： 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。
输入 s = “leetcode”, wordDict = [“leet”, “code”]。返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。

Set<String> set = new HashSet(wordDict);     // 直接用数组构建set
boolean[] dp = new boolean[s.length() + 1];  // 考虑dp数组长度和元素意义！！
Arrays.fill(dp, false);
dp[0] = true;                                // 注意初始情况！！
for(int i = 1; i <= s.length(); i++) {
    for(int j = 0; j < i; j++) {
        if(dp[j] && set.contains(s.substring(j, i))) {
            dp[i] = true;
            break;
        }
    }
}
return dp[s.length()];

2020-09-06

C++ 基础

Cpp 是一种通用编程语言，它扩展了 C 语言，加入了面向对象编程的特性。

数据类型

数据类型
1. 简单类型
  - 基本类型：
    - 整型：int通常是机器的最自然大小，占4B。short：短整数 2B。long：长整数，4 或 8B(取决于编译器和系统)。long long：长长整数，至少64位(8 byte)。INT_MIN = -2147483648 = 1 + INT_MAX
    - 浮点型：float 单精度浮点数 4B；double双精度 8B；long double 8B 或 16B。
    - 字符型：C++ 中表示字符的基本类型char，通常是 1B。字符用 ASCII 编码，以 ASCII 值参与运算
    - 空类型 void
  - 用户定义类型：枚举类型 enum
2. 结构类型：数组 [ ]，结构 struct，联合 union，类 class
3. 指针类型（*）
  
  类型长度（字节）表示范围备注
  
  char 1 -128 ~ 127 -2^7 ~ 2^7-1
  
  int 4 -2147483648 ~ 2147483647 -2^31 ~ 2^31-1
  
  double双精度型 8 -1.710^308 ~ 1.710^308 15位有效数字

十六进制[hexadecimal]：使用数字 0-9 和字母 A-F（或 a-f）来表示数值，每个十六进制位对应四个二进制位。

1
2

int hexValue = 0x1A3F;        // 0x 表示十六进制，用位运算进行十六进制的操作，输出时显示为二进制
cout << hex << value << endl; // 使用iomanip中的 hex 控制符来设置输出为十六进制格式

ASCII码：是一种将字符映射到数字的编码标准。ASCII码用于表示键盘上的字符，每个字符都对应一个唯一的数字。
0-“\0”(空字符,字符串结束标志)、9-“\t”(制表符：四个空格)、10-“\n”(换行符)、32-“ “(空格)
48-“0”(字符0)、65-“A”、 97-“a” 大小写差32（tolower()大写字符转换为小写）
转义字符 “\ character”：以 “\” 为前缀，表示改变后面 character 符号或整数值的意义，使其成为控制符或字符值。
char16_t：UTF-16字符类型。 char32_t：UTF-32字符类型。char16/32_t 是引入的字符类型，用于支持 Unicode 字符。

类型转换

int a = 65; string b = '9', s = "80";
char c = (char)a;         // ASCII -> char: 65 -> '65' 类型强制转换或显式转换
char d = a + '0';         // int -> char: 65 + '0' -> '65'
int e = b - '0';          // char -> int: '9' - '0' -> 9
int f = stoi(s);          // string -> int
string g = to_string(a);  // int - > string

常量
- 字面常量：字面常量是源代码中的常量值。例如，整数字面常量（ 5、-10）、浮点数字面常量（ 3.14、-0.001）、字符常量（'a'、'B'）、字符串字面常量（"Hello"、"C++"）等。值在程序编译时就已经确定。
- const 关键字创建的常量：在C++中，可以使用 const 关键字创建常量变量。这些变量在声明时被初始化，并且一旦被赋值后就不能再修改其值。例如：const double PI = 3.14159;
- 枚举常量（Enumeration Constants）：使用 enum 关键字定义的枚举类型也可以产生常量。枚举常量是一组具有整数值的符号常量。例如：enum Day { MON, TUE, WED, THU, FRI, SAT, SUN };

数据访问

名访问：程序被编译后，系统对已声明对象保存一张名表，登记对象的属性 < 名字，类型，地址 >

地址访问

double  b  // < b, double, 0X0066FDEC >
&b         // 取对象b的地址	
b          // 访问对象b	
*(&b)      // 间址访问

指针变量：能够存放对象地址的变量。定义形式：类型 * 标识符 ;

1
2
3

int * iptr; // iptr 是指向整型对象的指针，可以存放一个整型变量的地址
char * s ;	  // s 是指向字符对象的指针
int  ** p2;  int  * p1;  int  i = 3;  p1 = & i;  p2 = & p1; // 指向指针的指针

引用：引用说明为对象建立引用名，即别名；
- 引用在定义初始化时与对象名绑定，程序中不能对引用重定义；一个对象的别名，从使用方式和效果上与使用对象名一致
- 定义形式: 类型 & 引用名 = 对象名；
指向常量的指针：间址访问只读。定义形式：const 类型 * 指针或类型 const * 指针
指针常量：指针常量的值只能在定义的时候初始化。定义形式：类型 * const 指针
常引用：const 类型 & 引用名 = 对象名 ;

运算

类型转换：表达式求值之前，要对操作数进行必要的类型转换
1. 将短数扩展为机器处理的长度：参与算术运算的只有5种类型数据
  char、short -> int，unsigned char、unsigned short -> unsigned int，float -> double、long、unsigned long
2. 使运算符两端的操作数具有相同的类型： “向高看齐”，向表达能力强的类型转换；逐个算符转换
运算符的优先关系
- 单目运算符 > 乘除运算 > 加减运算 > 关系运算 > 逻辑与 > 逻辑或 > 赋值 > 逗号
- i + 1 < j * 4 && ! P || Q 等价于 : ( ( ( i +1 ) < ( j * 4 ) ) && ( ! P ) ) || Q
- P != i < j || Q && S 等价于 : ( P != ( i < j ) ) || ( Q && S )
自增、自减
- 前缀式：先增值后引用例：x = ++ i 相当于 i = i + 1 ; x = i ;
- 后缀式：先引用后增值例：x = i ++ 相当于 x = i ; i = i + 1 ;
- 自增、自减算符的运算对象只能是整型变量，不能为常量或表达式

位运算

16进制表示: 0xff -> 1111 1111

int a = 5, b = 3;        // a 二进制: 0101, b 二进制: 0011
int andResult = a & b;   // 0001 (1) 按位与 `&`
int orResult = a | b;    // 0111 (7) 按位或 `|`
int xorResult= a ^ b;    // 0110 (6) 按位异或 `^`
int notA = ~a;           // 1010 (-6 in two's complement representation) 按位取反 `~`
int leftShift = a << 1;  // 1010 (10) 左移<<：将操作数的每个位向左移动指定的位数，右侧用零填充
int rightShift= a >> 1;  // 0010(2) 右移>>：每个位右移指定位数，左侧用符号位(对于有符号数)或零填充

程序控制结构

所有程序都只能包含三种控制结构：顺序结构、选择结构和循环结构
if 语句，while语句，do-while语句，for语句

switch语句：根据一个整型表达式的值决定程序分支

switch(表达式)
{   case 常量表达式 1 : 语句 1  // case 标签是用来匹配 switch 后面表达式的值，执行相应的代码
    …
    case 常量表达式 n : 语句 n
    default : 语句 n+1        // 如果没有任何一个 case 匹配成功，用 default 标签来执行默认的操作
}

表达式类型为非浮点型；各常量表达式类型要与之匹配；各常量表达式要求各不相等；default 子句可选。
缺省时，没有匹配值 switch 语句为空
case 和 default 仅起语句标号作用，不能控制程序流程；一旦选中一个case分支后，将继续往下顺序执行（剩余所有）语句序列。添加 break 语句可以跳出 switch 语句体，达到控制流程作用

函数

库函数：预定义的函数，它们提供了各种功能，可以通过包含相应的头文件来使用。
C++标准库是一个包含许多有用函数和类的集合，可以使用这些函数和类来构建程序，而不必从头开始编写所有功能。
iostream 是一个C++标准库的头文件，提供了输入输出操作，包括 cin 和 cout。
cmath 是另一个头文件，提供了数学函数如指数函数pow(10.0, 2)、平方根sqrt()、三角cos()、绝对值abs() 等。
algorithm 中含有sort()、reverse()、swap()等函数。
string 是一个代表字符串string的类，它封装了许多处理字符串的函数和操作符。如substr()、find()函数等。
vector vec.size()获取 vector 的大小

命名空间：是用于组织代码标识符（如变量、函数、类等）的一种方式，以避免命名冲突。命名空间允许你在不同的命名空间中定义相同名称的标识符，从而使不同部分的代码可以使用相同的名字而不会产生冲突。C++标准库中的函数和类通常被放置在一个叫做 std 的命名空间中。你可以使用命名空间限定符 std:: 来访问其中的成员。

1
2

#include <iostream>     // 这是一个预处理指令，用于包含C++标准库中的 `iostream` 头文件。这个头文件包含了用于输入输出的流对象（如 `cin` 和 `cout`）以及其他相关函数。
using namespace std;    // 这是一个命名空间声明。`std` 是C++标准库的命名空间，包含了许多标准函数、对象和类。通过使用 `using namespace std;`，你可以在代码中直接使用 `cout` 和 `endl`，而无需在前面加上 `std::` 前缀。注意，虽然使用 using namespace std; 可以简化代码，但在大型项目中，为了避免命名冲突，可能会选择显式地使用命名空间限定符。

函数定义形式：类型函数名（形式参数表） { 语句序列 }
函数调用形式：函数名（实际参数表）
函数原型：作用是告诉编译器有关函数的信息：函数的名字、函数返回的数据类型、函数要接受的参数个数、参数类型和参数的顺序；编译器根据函数原型检查函数调用的正确性。函数原型的形式：类型函数名（形式参数表）;
函数参数的传递：值传递，指针传递，引用传递
传值参数：调用函数时，实参表达式的值被复制到相应形参标识的对象中，并按形参类型强制转换；函数内对形参的访问、修改，都在形参的标识对象进行；函数返回时，形参对象被撤消，不影响实参的值；值传送的实参可以是常量、有确定值的变量或表达式；函数返回值通过匿名对象传递

丨函数 FunctionObj 丨数据 DataObj 丨数组 DataObj

地址丨FunctionObj、&FunctionObj、FunctionObj、&FunctionObj 丨&DataObj 丨第i行第j列元素：a[i]+j、*(a+i)+j、&a[i][j]
函数、应用程序是编译器处理的对象，每一个函数模块都有一个首地址，称为函数的入口地址。
函数调用：找到函数入口地址；传递参数。函数入口地址：就是不带括号的函数名。
函数指针：指向函数的指针变量，值为函数的入口地址。函数的类型是函数的接口，可以通过指针变量的间址方式调用函数
- 若有函数类型为：double ( double, double ) ; 或 typedef double functionType ( double, double ) ;
- 定义指向这类函数的指针变量：double ( * fp ) ( double, double ); 或 functionType * fp1 , * fp2 ;

结构

结构由数目固定的成员构成，各成员可以具有不同的数据类型，一个结构变量在内存占有一片连续的存储空间

结构类型定义形式为：

struct  标识符
{  类型   成员1 ;
   …
   类型   成员n ;
};

可以用不同方法定义一个结构变量：(1) 声明类型之后声明变量 (2)声明类型的同时声明变量 (3)直接声明结构类型变量
访问结构变量的成员：（1）结构变量.成员（2）结构指针 -> 成员， (*结构指针 ) . 成员

STL

C++的STL（Standard Template Library，标准模板库）是C++标准库的一部分，它提供了一组通用的模板类和函数，用于实现常见的数据结构和算法。STL的设计目标是提供高效、通用、可复用的组件，以帮助开发者编写更加优雅和高效的C++代码。

容器（Containers）：容器是用于存储和管理一组对象的类模板。STL提供多种容器，每个容器都有不同的特性和适用场景。
vector：动态数组，支持快速的随机访问，底层实现是array，封装后使用更友好。list：双向链表，支持在任意位置插入和删除元素。deque：双端队列，类似于动态数组。map：关联数组，使用键值对存储数据。set：集合，存储不重复的值。

vector<int> dp(cost.size() + 1);               // 指定数据类型、数组大小
vector<vector<int>> dp(3, vector<int>(4));     // 创建一个包含3行4列的二维 vector
vector<int> vec = {1, 2, 3};  
sort(vec.begin(), vec.end());                  // 利用迭代器排序
vec.push_back(4);  vec.pop_back();             // 添加数据、移除末尾元素

算法（Algorithms）：STL提供了一组强大的通用算法，这些算法可以用于各种容器类型。这些算法涵盖了排序、查找、遍历、变换等多种操作。一些常见的算法包括： sort：对容器中的元素进行排序。find：在容器中查找特定元素。for_each：对容器中的每个元素执行操作。transform：将容器中的元素进行转换操作。
迭代器（Iterators）：迭代器用于遍历容器中的元素，提供了统一的访问接口，使得代码更具可扩展性。迭代器分为多种类型，包括输入迭代器、输出迭代器、前向迭代器、双向迭代器和随机访问迭代器。(begin()、end()、++、–、* 、== 和 !=)
函数对象（Function Objects）：函数对象是类的实例，可以像函数一样被调用。STL的算法和其他组件允许你使用函数对象来执行操作，或者使用标准库提供的一些预定义的函数对象。
适配器（Adapters）：适配器是用于转换或扩展容器或迭代器接口的类模板。例如，std::stack 是一个基于双端队列的堆栈容器适配器，std::queue 是一个基于双端队列的队列容器适配器。

输入输出

通常通过标准库中的 iostream 完成，包括 cin 用于从用户获取数据， cout 向屏幕输出数据，endl 输出一个换行符。
格式化输出：用到 iomanip 库
setw 和 setfill：这两个函数可以用来设置输出的宽度和填充字符。
1
cout << setw(6) << setfill('0') << 42; // 将数字 42 输出为 "000042"，总宽度为 6，使用 '0' 填充
fixed + setprecision：用于输出指定小数位数的浮点数。
1
cout << fixed << setprecision(2) << 3.1415926;

如果要处理多行输入可以使用 getline 函数，需要包含 iostream 头文件

#include <sstream>
string input; 
int number;
getline(cin, input);         // 读取整行输入：1 -1 -1 0
istringstream ss(input);     // 使用 istringstream 来分割数字
while (ss >> number) {```}   // 逐个获取数字

数据结构与算法

时间复杂度

时间复杂度是一种用来衡量算法运行时间与输入规模之间关系的概念。它不是用来精确测量程序运行时间的，而是描述在输入规模变化时，算法运行时间的增长趋势。
大O表示上界，当用它作为算法的最坏情况运行时间的上界，就是对任意数据输入的运行时间的上界。
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!)

数组

数组（Array）是有序的元素序列。数组是一种固定大小的数据结构，用于存储相同类型的元素。在C++中，数组的长度在创建时就固定了，无法在运行时改变。数组的元素是连续存储在内存中的，可以通过索引访问。数组有一些限制，例如长度固定、不能动态扩展等。当数组作为函数参数传递时，实际上传递的是指向数组首元素的指针。
1
int myArray[5]; int numbers[3] = {10, 20, 30}; int matrix[3][3] = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}; // 声明并初始化一个整数数组
在C++中，动态声明数组意味着在运行时根据需要分配数组的内存空间，而不是在编译时固定数组大小。
使用指针声明数组： 首先，你需要声明一个指针变量，该指针变量将用于存储动态分配的数组的地址。然后，使用内存分配函数（如 new 或 malloc）分配所需大小的内存空间。
释放内存： 在不再需要数组时，必须手动释放分配的内存，以避免内存泄漏。使用 delete 或 free 来释放内存。
1
int* dynamicArray = new int[size]; delete[] dynamicArray; // 动态分配数组内存释放分配的内存
数组容器（Array Container）：在C++中，数组（Array）和数组容器（Array Container）是两种不同的数据结构，它们在用法和特性上有一些区别。数组容器是C++标准库中提供的一种数据结构，用于存储相同类型的元素，并提供了一些更方便的功能。
array 是一个数组容器，它在内部使用数组来存储元素，是一个类模板，具有类似对象的行为，可以使用成员函数和操作符进行操作，提供了更多的功能，如获取数组大小、迭代器、操作符重载等，还可以像其他C++容器一样与STL算法一起使用。
1
#include <array> array<int, 5> myArray; array<int, 3> numbers = {10, 20, 30}; // 声明一个包含3个整数的array

动态数组vector的底层实现是 array，严格来讲vector是容器，不是数组。

#include <vector>
vector<int> myVector = {1, 2, 3, 4, 5};   // vector<int> myVector(n)  大小为n的空vector
// vector<vector<int>> myMatrix(n, vector<int>(n, 0))  n阶二维vector
myVector.push_back(1);    // 或直接下标索引 myVector[0] = 1;
for (const int& value : myVector)  cout << value;  // for (int i=0;i<myVector.size();i++){..}
for (vector<int>::iterator it = myVector.begin(); it != myVector.end(); ++it)  cout << *it;
myVector.pop_back();
if (myVector.empty())  cout << myVector.size();

sort函数接受两个迭代器参数，即要排序的范围的开始和结束位置。排序默认是升序的，如果需要降序排序，可以使用 std::greater
() 作为第三个参数。在使用 sort 函数之前，请确保引入了
头文件。
1
2
sort(arr, arr + n);
sort(data.begin(), data.end(), greater<int>());

链表

处理头结点有两种方式：直接使用原来的链表来进行删除操作、设置一个虚拟头结点在进行删除操作。
使用 ListNode* cur = head 进行链表操作，不要直接使用头结点操作！！！
判断空指针为 if(ptr != nullptr) ，不要用 if(!ptr)
nullptr与NULL：NULL 是一个宏定义，通常被定义为整数 0，NULL 用于表示空指针存在一些问题，因为它实际上是一个整数，可能会导致类型不匹配和模糊的代码。nullptr 是 C++11 标准引入的新关键字，用于表示空指针，是类型安全的，可以隐式转换为任何指针类型，但不会导致模糊的类型问题。推荐在现代 C++ 代码中使用 nullptr 来表示空指针。
1
2
ListNode* head = new ListNode(5); // 初始化节点
delete head; // 删除节点，回收内存

哈希表

在C++中，哈希（Hash）是一种将数据映射到固定大小的散列值的技术。哈希函数将输入数据转换为散列值，这个散列值通常用于快速查找或存储数据。C++标准库提供了一些哈希函数和相关的数据结构，让你可以在自己的程序中应用哈希。

什么时候使用哈希法？当我们需要查询一个元素是否出现过，或者一个元素是否在集合里的时候，就要第一时间想到哈希法。

哈希容器（Hash Containers）：C++标准库提供了一些哈希容器，它们使用哈希函数来快速存储和检索数据。
unordered_set：基于哈希表的集合，用于实现无序映射。类似于 set，但具有更快的查找性能。set 是一个有序的容器，它存储一组唯一的元素。
unordered_map：基于哈希表的关联数组，不保持元素的插入顺序，类似于 map但具有更快的查找性能。map 是一个有序（按键的字典顺序）的键-值对容器，它存储一组唯一的键，并且每个键关联一个值。

unordered_map<Key, T> mapp;                 // 创建一个空的无序映射。
mapp[x]                                     // 直接访问指定键的值，如果键不存在，会创建一个新的键并初始化为默认值。
insert({key, value})   erase(key)           // 插入，删除一个键值对。
at(key)                                     // 访问指定键的值，如果键不存在会抛出异常。
find(key)                                   // 查找指定键，返回指向该键的迭代器，若不存在，返回mapp.end() 
empty()   size()                            // 检查是否为空；返回键值对的数量
begin()   end()                             // 返回迭代器，用于遍历所有键值对。
for (const auto& pair : mapp) {             // 范围循环,遍历所有键值对。
    cout << pair.first << pair.second;
}    
                                            // set的用法类似

字符串

访问 string 字符串特定索引位置的字符时，返回的类型是 char

直接使用 + 连接字符串和字符串string/字符char；
使用 ==、!=、<、<=、>、>= 比较字符串和字符串string/字符char；
使用cstring库中的字符串处理函数。其中，strcmp() 用于比较两个 C 风格字符串，strcpy()复制。

getline(cin, str)                            // cin以空格分隔string。而getline()会等待用户在终端输入一行字符串，然后将该字符串存储在 str 变量中。注意，getline() 会读取一行完整的输入，包括换行符，并且将换行符从输入中删除。
str.append(count, '0')                       // 在str末尾加上count个'0'
str.substr(i, 8)                             // 从位置i开始截取长度为8的str的子串
str.erase(i, 5);                             // 从位置i开始，删除5个字符
str1.compare(str2)                           // 逐字符比较字符串(字典顺序)大小，返回0/1/-1
reverse(s.begin() + 0, s.begin() + n);       // algorithm库字符串翻转函数，翻转范围[0, n-1]
void reverse(string& s,int start,int end){   // 自制字符串反转函数，reverse(str, 0, str.size()-1)
    for (int i = start, j = end; i < j; i++, j--)  swap(s[i], s[j]);    
}

栈与队列

我们常用的SGI STL，如果没有指定底层实现的话，默认是以deque为缺省情况下栈、队列的底层结构。
不允许有遍历行为，不提供迭代器。
所以STL 栈、队列不被归类为容器，而被归类为container adapter（容器适配器）。

栈（Stack）遵循后进先出（Last-In-First-Out，LIFO）的原则。 std::stack 容器用于实现栈。

#include <stack>
stack<int> myStack;               // 创建一个空的栈，存储整数
myStack.push(10);                 // 添加元素到栈
myStack.top();                    // 访问栈顶元素
myStack.pop();                    // 移除栈顶元素
while (!myStack.empty()) {...     // 遍历栈

队列（Queue）遵循先进先出（First-In-First-Out，FIFO）的原则。 std::queue 容器用于实现队列。

1 2	#include <queue> queue<int> myQueue; myQueue.push(10); myQueue.front(); myQueue.pop(); while (!myQueue.empty()) {...

`list`（双向链表）

std::list 是一个双向链表容器，每个元素都包含一个指向前一个元素和一个指向后一个元素的指针。这使得插入和删除操作在链表中非常高效，但随机访问较慢。以下是一些 std::list 的常见用法：

#include <list>
    std::list<int> myList;
    myList.push_back(1);                                 // 插入元素
    myList.push_front(2);          
    myList.insert(std::next(myList.begin()), 3);         // 在迭代器位置后插入
    myList.pop_back();                                   // 删除元素
    myList.pop_front();
    myList.erase(std::next(myList.begin()));             // 删除迭代器位置的元素
    for (const int& item : myList) { cout << item,,      // 遍历元素

`deque`（双端队列）

deque 是双端队列容器，支持在两端进行高效的插入和删除操作，并且允许随机访问。它的特性使得它在需要在两端进行频繁操作的场景下很有用。以下是一些 deque 的常见用法：

#include <deque>
std::deque<int> myDeque;
myDeque.push_back(1);                                   // 插入元素
myDeque.push_front(2);  
myDeque.pop_back();                                     // 删除元素
myDeque.pop_front();
myDeque.push_back(3);                                   // 随机访问
myDeque.push_back(4);
int value = myDeque[1];                                 // 访问第二个元素，值为4
for (const int& item : myDeque) { cout << item ;;;      // 遍历元素
}

`Heap`（堆）

在 C++ 中，你可以使用 priority_queue 来实现小顶堆和大顶堆。默认情况下，priority_queue 是大顶堆，但你可以通过改变比较函数来实现小顶堆或大顶堆。

实现大顶堆：

#include <queue>
// 创建一个大顶堆（默认情况）
priority_queue<int> maxHeap;
// 向大顶堆中插入元素
maxHeap.push(5);    maxHeap.push(2);    maxHeap.push(8);    maxHeap.push(1);
// 访问堆顶元素（最大值）
cout << "最大值：" << maxHeap.top() << std::endl;
// 弹出堆顶元素
maxHeap.pop(); ；；}

实现小顶堆：

#include <queue>
// 创建一个小顶堆
// 第一个参数 int：这是容器中存储的元素的类型，也就是小顶堆中的元素类型。在这里，我们使用 int 类型。
// 第二个参数 vector<int>：这是容器类型，用于存储小顶堆的元素。通常情况下，我们使用 std::vector 作为容器，但你也可以使用其他容器类型，比如 std::deque。
// 第三个参数 greater<int>：这是比较函数对象，用于定义小顶堆的比较规则。在这里，greater<int> 是一个函数对象，它表示比较时采用递增的方式，即根节点的值小于子节点的值。
priority_queue<int, vector<int>, greater<int>> minHeap;
// 向小顶堆中插入元素
minHeap.push(5);  minHeap.push(2);  minHeap.push(8);  minHeap.push(1);
// 访问堆顶元素（最小值）
cout << "最小值：" << minHeap.top() << std::endl;
// 弹出堆顶元素
minHeap.pop();；；}

二叉树

二叉树（Binary Tree）是一种常见的树状数据结构，其中每个节点最多有两个子节点，通常称为左子节点和右子节点。每个节点都存储一个值，这个值可以是任何类型，取决于树的应用。
1
2
3
4
5
struct TreeNode {
int val;
TreeNode *left, *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则为满二叉树。
完全二叉树：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点。
优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。
二叉搜索树 BST：具有有序性质，适用于快速查找、插入和删除操作。
若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树
平衡二叉搜索树 AVL： 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn。
而unordered_map、unordered_set底层实现是哈希表。

2020-09-01

Shots 📷

理念

构图，色彩，内容，摄影艺术
审美，美是理念（客观真实）的感性显现
生命力（动物拟人
拍照要有情感，不要刻意捕捉和渲染苦难，没有价值没有温度没有同理心
构图是为了故事呈现/画面表达服务的
技术是基础接下来对自己生命情感的一个探索把自己的理性和感性相交融成为摄影的灵性
看一张照片 don’t think、feel、、快速四五条分析，用摄影师的眼光来解读，审美
摄影-习惯快门-快感积累-质变
用时间拍照用时间沉淀
纪实摄影（对人的训练记录时间记录那一刻对世界的真实表达摄影的冲动
艺术性不是生活的复制品艺术的摄影点-生活化趣味性情绪化幽默化 -耐人寻味
距离感（全身和特写表达不同的情感
手是人的第二张脸（外在美，情感，信息

构图

大多数照片较为平稳，同时有一些张力
物体的数量、大小、色彩、位置、方向、质感、吸引力会影响其视觉重力，画面中多个物体的视觉重力构成了平衡与张力。
平衡来源：静态，对称，稳定，横平竖直，客观
张力来源：动态，不对称，边角，斜线，情感
平面秩序: 事物变图形抽象
照相不是出于构思作画，而是出于选择构图。三维世界在二维照片中有了原来不存在的关系（远近透视）
决定性瞬间:照片只叙述当下，恰好一个瞬间所有事情(人,地,物,所有细微之处)均各得其所，并同时展现出特定内涵和意义
布列松:“如果照片是为了最大程度上让人理解其被摄对象那么形式关系必须被严格地建立起来摄影的目的是在真实事物所构成的世界中甄别出韵律在一张照片中构图是同时发生的综合结果是对于眼之所见的各元素的有机协作。”
形式即内容但形式也离不开内容（不要只会拍老头环卫外卖小哥）

曝光

曝光三要素：光圈，快门速度，感光度iso，与图像亮度有关
另外，光圈与景深相关，快门与凝固程度有关，感光度与图像细腻程度有关；
M档手动挡（手动调节三要素），A档光圈优先（调节光圈和iso自动设置快门），S档快门优先（调节快门和iso自动光圈）
光圈：控制镜头进光量(通过镜头前面看得到光圈大小)，其数值等于 焦距/通光直径
光圈越大数值越小，进光量越大，背景虚化越强，1.4 - 2 - 2.8 - …表示光圈半径差根号2倍光圈面积差2倍进光量差一倍曝光差一档
景深指的是画面中清晰的一段(否则就被虚化)，光源与镜头（光圈）形成的角度越大，景深越小，所以，景深与被摄物体距离平方成正比，与光圈数值成正比，与镜头焦距平方成反比
安全快门：在光圈开到最大，快门尽量慢时，拉高iso（后期去除噪点）做到正常曝光，拍出来不糊（因为手抖）的快门。
安全快门的经验值是 1/焦距（远距离的狙击枪对瞄准的要求高），这里前提默认被摄对象是静止的。
快门速度应该考虑被摄体的移动速度，动态人像快门通常不能低于1/200，还需考虑其与相机的距离（影响其在画面中的比例）
拍摄“背景清晰，行人模糊”：打开相机防抖，保持手的稳定，快门设置在1/30或1/50
拍摄“背行人清晰，背景模糊”：关闭防抖，相机跟随物体，移动的同时按下快门
iso：感光度指传感器对于光线的敏感程度，相当内置光源，数值越大噪点越大（牺牲图像细腻程度）事实上，是由于低进光量带来的噪点，只是iso提高亮度后使噪点更加清晰
iso只是一个配合的角色，90%的情况下应该自动（由曝光补偿控制）即可
曝光补偿：事实上还是通过支配三要素来控制曝光。
当m档时，曝光补偿是三要素的调整后的画面整体曝光偏向，做信息提示用。
当三要素自动/半自动时，曝光补偿就是一个总控开关，我设置这个开关为-1，其他三要素就根据这个指令自动计算结果。
最起码的是亮度正常，看直方图（牢理论：暗处不死黑，高光不过曝）
测光功能：平均测光模式下，如果相机计算图像中所有像素的平均亮度为18度灰，则认为曝光补偿为0（前提是相机认为所有物体的平均反射率都是18%，自然界中物体的平均值确实如此，但对于具体物体不一定准确，需要调整曝光补偿，白加黑减）
不同的测光模式，区别只在采样范围(整体，中心，点)，使得曝光补偿为0时采样范围内平均亮度为18度灰
一般来说，无需改变测光模式，在多重测光（索尼，富士）下调整曝光补偿即可。

透视

焦段越大，拍得远，画面窄（相同画面下，人靠近背景（事实上大焦段需要在距离主体更远处拍摄出相同画面））
焦段越小越广角人越胖。 c画幅的35mm等效全画幅50mm
85mm-人像焦段。 35mm-人文扫街呼吸感。 50mm-两者折中

透视关系：与焦段没直接关系，和镜头离物体远近有关。

焦段	距离	透视	效果
短焦	距离近	透视强	广角拉伸感有张力
中段	/	透视自然与人眼相似	没有明显拉伸感背景较平但没有明显压缩感
长焦	距离远	透视弱	背景比例接近真实压缩感

定焦镜头的画质一般比变焦镜头好，光圈可以更大
对焦: 对焦的过程就是把对焦点锁定在主体的过程。定焦镜头
对焦点，对焦性能，，对焦距离
手动对焦。。

器材

画质：相同传感器下，像素越大画质越差。。
传感器cmos: 手机<卡片机<半画幅<全画幅<中画幅<大画幅，大传感器成像更细腻噪点更少
相同距离下，取景范围：全画幅焦距 = 半画幅焦距 * 1.5(1.6)（半画幅50mm的取景范围相当于全画幅75mm的取景范围）
档位：M档手动挡（手动调节三要素），A档光圈优先（调节光圈和iso自动设置快门），S档快门优先（调节快门和iso自动光圈）
图像质量：FINE(直出jpeg)+RAW(无损照片)
动态范围，宽容度
宽容度一般指的是RAW原始数据，能记录最暗和最亮信息的范围。
动态范围则是指照片或视频，能保留最暗和最亮有效信息的范围。
你可以解一张高宽容度的RAW格式照片，用它调出一张高动态范围的照片，大致就是这个意思。
白平衡：相机白平衡等于光源色温时展现为白光，越低越黄（暖色），越高越蓝（冷光）

用光

硬光：太阳/小光源LED等离物体距离远，可以认为是平行光，能让物体产生清晰阴影的光，称为硬光。硬光会使画面显得精神、干脆，也会凸显脸上的沟壑、痘痘的高光。
柔光：随机的阴影模糊的光线。柔光会使脸部的光影过度更加柔和。硫酸纸、塑料袋等介质都能够冲散光线，在太阳前加柔光布，跳闪也是一种做法（打向天花板再均匀反射下来）原理都是让光线从规律变成随机。
光源距离主体越近，光线越柔和（发光面积越大？），光影的反差越大（平方反比定律，后期拉回来即可）
光柔与硬指的是光线的杂乱程度，体现在阴影的锐利程度上；反差的大小是指光面与阴影之间的亮度差异，体现在阴影的深浅。
直闪，热靴等，，
光比：背光面亮度/受光面亮度。“逆光时人脸是黑的”“演唱会时艺人的脸过曝”“窗外过曝”“背景太亮&太暗”等问题基本上都是由于主体受光和背景受光相差过大所导致的，无法通过曝光三要素调整，因为相机的宽容度优先，只能展现一段的亮度。
解决方法：拍摄raw后期拉回来，拍摄两张不同曝光的图像合成，人像摄影给暗处补光，亮部和暗部放弃其一

参数

人的精力是有限的，拍摄中应该注重拍摄本身而不是相机的设置，需要适当放权由相机决定参数。
拍摄时，需要思考和权衡的只有：档位选择，曝光补偿，快门速度设定，保证安全快门，光圈设置
其他可以在拍摄现场外设置好的参数：照片格式的选择，白平衡的设置，防抖开启与否，测光模式的选择，对焦模式的选择，对焦区域的选择，连拍模式的选择，长时间曝光降噪与高iso降噪，色彩空间的选择，滤镜/创意外观
风光参数
光圈: 白天建议光圈优先此时快门速度不必担心，一定够快；如果近处有景物时，要缩小光圈(一般取f7.1以上)；近处无景物而对焦点较远时，光圈可大可小。
快门: 夜晚建议快门优先。光线不足且手持时首先保证富裕的安全快门上三脚架时，可选慢快门，使得水、云等呈现丝绸状。
其他: RAW格式、ISO自动、白平衡自动、单次对焦、单点对焦如果没有快门线，设置2秒的延迟快门
扫街参数
光线不稳定时，快门优先:1/200以上，保证移动的主体也清晰。
在光照很强时，可用光圈优先，设置大光圈，快门速度自然会很高
对焦: 区域选广域，来不及调整对焦点；模式选AFC连续对焦，锁住移动主体;
其他:光圈与ISO自动、曝光补偿控制亮度、白平衡自动。篮球赛、活动、会议类似。。
参数设定整体思路
白天光线充足时，安全快门不必担心，可光圈优先:风光f8左右，人像开到最大。
光线不足时。安全快门压力大，可选快门优先，根据不同情况，设置不同的安全快门。
一般，快门速度越快越安全，但需要拍摄丝绸状流水时，须设置慢快门，用三脚架固定，别忘记套上ND镜。
拍摄移动、随机主体时，对焦选择广域+AFC连续对焦，把对焦交给相机;拍摄风光、产品时，可选单点+单次对焦，精确把控。
测光模式保持默认不必调来调去，白平衡可前期设置好，也设置自动后期调整。

后期

RAW：无损照片，保留最多信息
Ligthroom

类型	长度（字节）	表示范围	备注
char	1	-128 ~ 127	-2^7 ~ 2^7-1
int	4	-2147483648 ~ 2147483647	-2^31 ~ 2^31-1
double双精度型	8	-1.710^308 ~ 1.710^308	15位有效数字

SpringFramework没有解决了什么问题？

SringBoot的概述

SpringBoot 注解

核心功能和特点

Spring Framework

Core Container（Spring的核心容器）

Data Access/Integration（数据访问／集成）

Web模块

AOP、Aspects、Instrumentation 和 Messaging

Test模块

结合Spring历史版本和SpringBoot看发展

控制反转(IOC)

切面编程(AOP)

SpringMVC请求流程和案例

拦截器

Spring 事务管理

统一异常处理

Spring Security

理论基础

多线程的出现是要解决什么问题的?

线程不安全是指什么?

举例说明并发出现线程不安全的本质什么? 保障 可见性，原子性和有序性。

Java是怎么解决并发问题的? 3个关键字，JMM 和 8个 Happens-Before

线程安全是不是非真即假?…不是

线程安全有哪些实现思路?

如何理解并发和并行的区别?

线程基础

进程、线程、纤程

线程有哪几种状态? 分别说明从一种状态到另一种状态转变有哪些方式?

通常线程有哪几种使用方式?

基础线程机制有哪些?

线程的中断方式有哪些?

线程的互斥同步方式有哪些? 如何比较和选择?

线程之间有哪些协作方式?

Java锁

CAS

对象的内存布局？？

共享模型之管程

synchronized 解决方案

线程安全分析

Monitor

wait/notify

线程状态转换

活跃性

Lock

非共享模型

JUC 类汇总

Java 线程池 ？？

JVM 跨平台原理

JVM 知识要点

类的生命周期

JVM 类加载

类字节码详解

类加载器

JVM类加载机制

双亲委派机制

打破双亲委派机制：

JDK8 后的类加载器

JVM 内存结构

程序计数器

Java 虚拟机栈

本地方法栈

**栈是运行时的单位，而堆是存储的单位**

堆

方法区

直接内存

Java 内存模型

JVM GC 垃圾回收

方法区的回收

堆的回收

五种引用

垃圾回收算法

分代垃圾回收算法

垃圾回收器

G1收集器

JVM 排错调优

JVM 知识体系

数组

Arrays

Vector

举例说明并发出现线程不安全的本质什么? 保障可见性，原子性和有序性。

Java 线程池？？

`栈是运行时的单位，而堆是存储的单位`

面向对象三大特性

`Java中的引用`不是直接的内存地址，而是对实际对象的间接引用。这使得Java程序员不需要关心内存管理，因为Java虚拟机（JVM）会自动管理对象的创建和销毁。